Questão 1072546

• Banca: VUNESP
• Órgão: UNESP
• Ano: 2013
• Provas: VUNESP - 2013 - UNESP - Vestibular - Primeiro Semestre
• Disciplina: Matemática
• Assuntos: Polinômios

Sabe-se que, na equação x³ + 4x² + x – 6 = 0, uma das raízes é igual à soma das outras duas. O conjunto solução (S) desta equação é

• A. S = {– 3, – 2, – 1}
  
• B. S = {– 3, – 2, + 1}
  
• C. S = {+ 1, + 2, + 3}
  
• D. S = {– 1, + 2, + 3}
  
• E. S = {– 2, + 1, + 3}

Gabarito: B

Comentários

• Tem alguma outra forma de resolver essa questão sem ser substituindo os valores?

  
  

  Por recado pra mim, fico grato. :)

• 
  
  

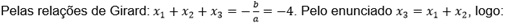
                                                               2x₃ = - 4 → x₃ = - 2 
  
  

  Então o polinômio de grau 3 será divisível por x + 2, aplicando o método de Briot-Ruffini:
  
  

                                                                
  
  

  Resolvendo x³ + 4x² + x - 6 = 0 → (x + 2) (x² + 2x - 3) = 0 → x = -2 ou x = 1 ou x = -3 

  
  

  Letra B

• Se levarmos em conta que para dar esses valores, temos de ter 2 raízes negativas e 1 positiva, para que dê certo na decomposição, auxilia nas tentativas

  Ex: x-(-x1)= (x+x1)

  LETRA B

  (x-(1))=( x-1)

  (x-(-2))=(x+2)

  (x-(-3))= (x+3)

  (x-1).(x+2).(x+3)

  x³+4x+x-6=0

• x^3 + 4x^2 + x – 6 = 0

  Raízes:

  x1=x x2=y x3=z

  O enunciado diz q a soma de duas raízes igual à terceira, ou seja x+y=z.

  Pela propriedade de soma de raízes temos:

  x+y+z = -b/a

  x+y+z= -4/1

  z + z= -4

  2z = -4

  z=-2

  Analisando as alternativas somente as letras A e B tem -2 como solução, sendo q somente a alternativa B satisfaz o q diz o enunciado (x+y=z), portanto, alternativa correta letra B.