-
Não é questão de elétrica, e sim de matemática.
Cada captor deve responder pela mesma área de cobertura, ou seja, 8 x 6 m. Nessa área de atuação de um captor, temos que garantir que a proteção "varra" todos os pontos da cobertura, inclusive seus vértices. A condição mínima de ocorrência disso seria uma área de proteção representada por uma circunferência circunscrita ao retângulo. O raio dessa circunferência seria a hipotenusa de um triângulo cujos catetos são representados pela metade de cada lado do retângulo: 3m e 4m; logo, R = 5m
Dado o ângulo de proteção igual a 30º, temos:
tg 30 = 5 / h
h = 5 * (raiz de 3)
-
A tg 30 é (raiz de 3)/3 e não (raiz de 3)
-
Mikaela está certa, tg30 é raiz(3)/3.
Acredito que a resolução da questão é exatamente como muito bem explicou o Ricardo Palhares. Contudo, acho que o âgulo de proteção de 30º é formado entre a altura (h) e a hipotenusa.
Assim sendo, o ângulo formado entre a base (raio de 5 m da circunferência) e a hipotenusa é 60º, logo:
==> tg60 = h / 5
==> raiz(3) = h / 5
==> h = 5 * raiz (3)
-
Cada captor deve responder pela mesma área de cobertura, ou seja, 8 x 6 m. Nessa área de atuação de um captor, temos que garantir que a proteção "varra" todos os pontos da cobertura, inclusive seus vértices. A condição mínima de ocorrência disso seria uma área de proteção representada por uma circunferência circunscrita ao retângulo. O raio dessa circunferência seria a hipotenusa de um triângulo cujos catetos são representados pela metade de cada lado do retângulo: 3m e 4m; logo, R = 5m
Dado o ângulo de proteção igual a 30º, temos:
tg 30 = 5 / h
h = 5 / (raiz de 3 / 3)
h = 5 x 3 / raiz de 3
h = 15 / raiz de 3 ( fazer racionalização)
h = 5 * (raiz de 3)
-
Antes de calcular a altura
dos captores, é preciso entender o problema, isto é, compreender a posição dos
para-raios e do ângulo de proteção. Visto isso, dado que a edificação possui 16
m de comprimento e 6 m de largura, é preciso dividir os dois para-raios
nessa área.
A Figura 1 apresenta a posição
dos para-raios em planta e uma vista representando a altura dos captores
(H).
Figura 1: Situação do
problema. Medidas em metros.
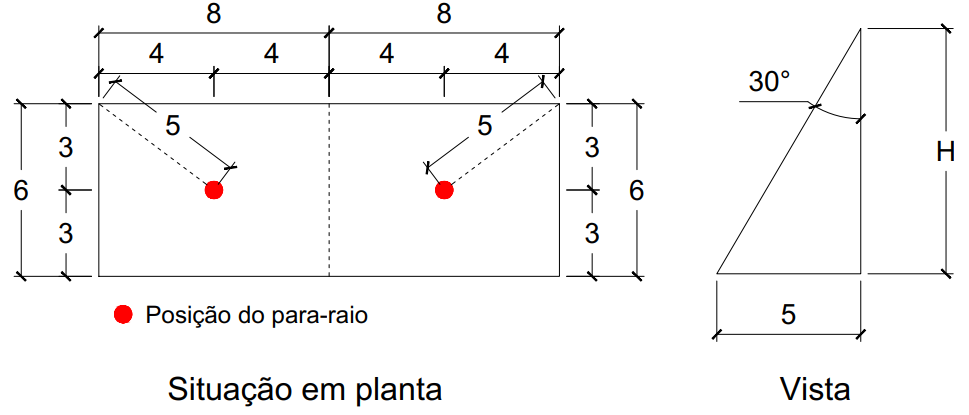
A Figura 1 evidencia que a
máxima distância entre ele o ponto mais distante (o vértice da edificação) é
igual a 5 m. Ela consiste na hipotenusa de um triângulo com catetos medindo
3 m e 4 m:
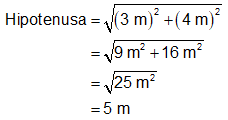
Visto isso e ainda pela
Figura 1, tem-se que a altura dos captores (H) relaciona-se da seguinte
maneira com o ângulo de proteção e a distância máxima entre ele e o vértice
mais distante:
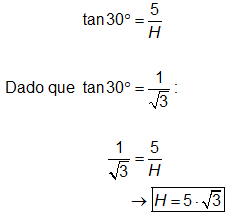
Assim, a altura dos
captores é de 5√3 m e, portanto, a alternativa A está correta.
Gabarito do Professor: Letra
A.
-
Esse cara fez:
https://youtu.be/zllBR4RTxxs