-
Nas minhas contas só acha 0,04, Alguém sabe resolver?
-
Provavélmente você esqueceu de que o 2% deve ser dividido por 100...
-
S= 2*K*L*I/%queda de tensao*Un
K= resistividade do cobre = 1/58
L= comprimento 23,2 m
%queda de tensao = 2%=0,02
Un= 110 v
I= p/v= 1210/ 110 = 11
S = 2*1/58*23,2*11/110*0,02 = 4
-
ΔU% = ΔU / U >> ΔU = ΔU% . U >> ΔU = 0,02 . 110 >> ΔU = 2,2 V
U = R . i
R = (ρ . L) / A - Resistência do condutor
ΔU = (ρ . L . i) / A >> A = (1/58 . 23,2 . 11) / 2,2 >> A = 2 mm²
Considerando que na ligação monofásica:
a) 1 fase e 1 neutro
b) fase e neutro de mesma bitola
Portanto: Atotal = 2 . A >> Atotal = 4 mm²
LETRA E
-
S=2p*PL/(e%U^2) = 2*1/58*1210*23.2/(0.02*110^2)=4 mm²
Substituir quando trifásico por raiz(3) e a distancia multiplica-se por raiz(3)/2
-
A área a seção transversal da fase, em circuitos monofásicos, pode ser calculada por:
A = (2p x L x I) / (DV x V)
A - área da seção (mm²);
p - resistividade elétrica (ohm.mm²/m) = 1/58;
L - comprimento do condutor (m) = 23,2m;
I - corrente (A);
V - tensão (V) = 110V;
DV - queda de tensão admissível (decimal) = 2% = 0,02.
No exercício temos todas as variáreis, menos a corrente, porém calcula-se a corrente pela seguinte fórmula:
P = V x I
Onde:
P - potência elétrica (VA);
I - corrente (A);
V - tensão (V) = 110V;
A potência usada para cálculo de circuitos é a potência aparente(Pap) cuja unidade é o Volt-Ampére (VA), o exercício deu a potência ativa(Pat) cuja unidade é o Watts (W). Para transformar uma em outra basta utilizar o fator de potência (FP):
FP = Pat / Pap
1 = 1210 / Pap
Pap = 1210 VA
Retornando a fórmula anterior:
P = V x I
1210 = 110 x I
I = 11 A
Retornando a fórmula inicial:
A = (2p x L x I) / (DV x V)
A = (2 x 1/58 x 23,2 x 11) / (0,02 x 110)
A = 4mm²
Portanto, gabarito letra E.
Fonte: NBR 5410
-
S = PLIK/QU , onde P = 2
S= 2 x 23,2 x (1210/110) x 1/58 / 0,02 x 110 = 510,4/127,60 = 4mm2
-
Para solucionar essa
questão precisamos colocar em prática nossos conhecimentos instalações
elétricas. Especificamente, é preciso lembrar que a área da seção
transversal (A) da fase de circuitos monofásicos é calculada pela seguinte
equação:
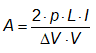
Em que p é a resistividade
elétrica do fio; L o comprimento da fase; I a corrente elétrica; ΔV a queda
percentual de tensão admissível para o circuito; e V a tensão.
Todas os dados foram fornecidos
diretamente pelo enunciado, com exceção da corrente elétrica. Entretanto,
tem-se que a potência elétrica (P) consiste no produto entre a tensão e
a corrente. Logo:
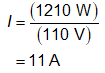
Substituindo esse valor e
os demais na equação para o cálculo de A, resulta que:
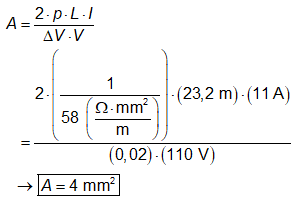
Portanto, a área
calculada para o condutor é de 4,0 mm². Logo, a alternativa E está
correta.
Gabarito do Professor: Letra E.