-
4 polegadas = 0,1016m
Q = V*A
Q ={ 2 * 3,14 * 0,1016²}/4 = 0,0162m³/s
0,0162m³/s* 1000 =~ 16 l/s
-
Q = V * A
Q= ?
V = 2 m/s
A = 3,14 * 0,0508 ² m = 8,1 X 10 ^-3 m²
Q = 2 m/s * 8,1 X 10 ^-3 m²
Q = 1,62 X 10 ^-2m³/s
1 m³ -------------------------- 1.000 L
1,62 X 10 ^-2 m³ ---------- X
X = 16,2 L/s
-
Para solucionar essa
questão precisamos colocar em prática nossos conhecimentos sobre Hidráulica.
A vazão (Q) de uma
tubulação trabalhando a seção cheia consiste no produto entre a área da seção
transversal da tubulação (A) e a velocidade do fluxo de água (V).
Matematicamente, tem-se que:
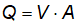
Devemos lembrar ainda
que:
·
Uma polegada equivale a 0,0254 m;
·
A área de uma seção circular é dada por π vezes o diâmetro (D) ao
quadrado dividido por quatro;
·
Um metro cúbico por segundo equivale a 1000 litros por segundo.
Visto isso e
substituindo os dados fornecidos pelo enunciado na equação acima, resulta que:
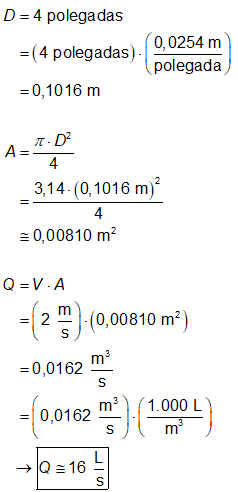
Logo, a vazão máxima
que pode passar pela tubulação é de, aproximadamente, 16 litros por segundo.
Portanto, a alternativa C está correta.
Gabarito do
professor: Letra C.
-
- 1" = 25mm (aproximadamente)
- 4" = 100mm (--//--)
Q = A x V
- Área = Pi x D²/4 (m²)
- Área = 3,14 x 0,1²/4 (m²)
- Área = 3,14 x 0,01/4 (m²)
Q = A x V
Q = (3,14 x 0,01/4) (m²) x 2 (m/s)
Q = (3,14 x 0,01/2) (m³/s)
Q = 0,0157 (m³/s) ou 15,7 (L/s) (o mais próximo 16 L/s)