-
NBR 7190: Projeto de estruturas de madeira
7.5.3 Compressão de peças curtas
Para as peças curtas, definidas pelo índice de esbeltez λ ≤ 40, que na situação de projeto são admitidas como solicitadas apenas à compressão simples, dispensa-se a consideração de eventuais efeitos de flexão.
Do problema, têm-se lambda = 40 e r = 2,2 cm.
Sabe-se que lambda = L/r, então 40 = L/2,2, L = 88 cm = 0,88 m
-
Índice de Esbeltez (λ)
λ = L / r
NBR 7190
Peças curtas -> λ < 40
Peças medianamente esbeltas -> 40 < λ < 80
Peças esbeltas -> 80 < λ < 140
Logo, para peças curtas, o comprimento será:
40 = L / 0,022m
L = 0,88m
Calma, calma! Eu estou aqui!
-
Gente, só uma duvida, eu fiz a questão, usando o conceito seguinte :
Em treliças de madeira, o λ máximo é 50 em peças tracionadas
e λ máximo é 40 em peças comprimidas.
A partir dai joguei na fórmula do índice de Esbeltez e cheguei ao resultado, é um método certo ou cometi algum equivoco ?
-
Você confundiu os conceitos. Esses valores de 40 e 50, respectivamente para compressão e tração, dizem respeito à relação entre comprimento longitudinal e largura da seção transversal.
-
Então quer dizer que :
comprimento longitudinal / largura da seção transversal = 50 nas peças tracionadas
comprimento longitudinal / largura da seção transversal = 40 nas peças comprimidas
Esse conceito seria isso ?
-
Para responder essa
pergunta devemos colocar em prática nosso conhecimento sobre estruturas de
madeira.
Primeiramente é
importante conceituar que o raio de giração se trata de uma propriedade
geométrica muito utilizado no estudo da flambagem, sendo calculado pela raiz
quadrada do quociente entre o momento de inércia e a área da seção transversal.
A ABNT NBR 7190 (1997),
intitulada “Projeto de estruturas de madeira" estabelece as condições de
projeto, execução e controle de estruturas de madeira. Em seu item 7.5.3, tal
Norma trata sobre a compressão de peças curtas, estabelecendo que “para as
peças curtas, definidas pelo índice de esbeltez λ ≤ 40, que na situação de
projeto são admitidas como solicitadas apenas à compressão simples, dispensa-se
a consideração de eventuais efeitos de flexão".
Lembrando que o índice
de esbeltez (λ) é definido como o quociente entre o comprimento de uma
peça e o raio de giração mínimo de sua transversal, para λ = 40 e r = 2,2
cm, calcula-se o máximo comprimento (L) que a peça pode ter para que apenas a
compressão simples seja considerada:
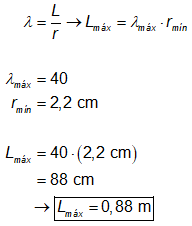
Logo,
para dispensar efeitos de flexão, a peça do problema pode ter um comprimento
máximo de 0,88 m.
Gabarito
do professor: Letra C.
-
Lambda = 40