raio de giro é igual a raiz quadrada da ( inércia dividido pela área )
I = bh³/12
A = b x h
quando vocês fizerem as contas vão encontrar 6/raiz quadrada de doze.
MULTIPLIQUEM EM BAIXO E EM CIMA POR RAIZ QUADRADA DE DOZE.
vai resultar no dividendo 6 vezes a raiz quadarda de doze; no divisor 12
voçês pegam o doze da raiz quadrada e simplifica para 2 ao quadrado vezes 3
com isso vamos ter 12 vezes raiz quadrada de três divido por 12 resultando em: raiz quadrada de três.(cm)
Para simplificar o Pcrit de Euler considerem : 1 Gpa = 100 Kn / cm2 ( meu teclado está com defeito no 2 elevado ).
Pcr= 3,14 x 3,14 x E x I / ( K x L)2- considerem ao quadrado.
K x L CHAMA-SE COMPRIMENTO EFETIVO
No nosso caso k = 1
Agora vocês vão pegar o E e transformar em Kn / cm2
Pcr= ( 3,14 x 3,14 x 20.000 x 6 x 6³/ 12) /( 200 x 200) = 3,14 x 3,14 x 54 Kn.
gabarito letra b
por que letra b?
raiz quadrada de 3cm é igual 10 x raiz quadrada de 3mm.
Para responder essa
pergunta devemos colocar em prática nosso conhecimento sobre Resistência dos
Materiais.
O raio de giro (r)
consiste na raiz quadrada da relação entre o momento de inércia (I)
e a área da seção transversal (A). Lembrando que o momento de inércia no
produto entre a base a altura ao cubo dividida por 12, calcula-se que:
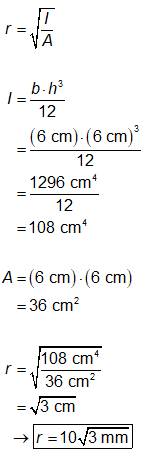
Por sua vez, a carga
crítica de flambagem de Euler (Pcr) é dada pela equação a
seguir:
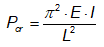
Em que E é o módulo
de elasticidade longitudinal do material, I o momento de inércia mínimo
e L o comprimento destravado. Visto isso e substituindo os dados do
problema na equação, resulta que:
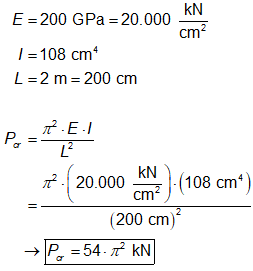
Portanto, a alternativa
B está correta.
Gabarito do professor: Letra B.