Para responder essa pergunta devemos colocar em prática nosso conhecimento sobre Topografia, especificamente sobre o cálculo de áreas.
A
Topografia trata-se de uma área responsável por estudar as
características naturais e/ou artificiais de um terreno, no contexto
altimétrico e planimétrico. A etimologia da palavra “topografia" deriva dos
termos gregos “topos" e “graphen", que significam, respectivamente,
“lugar" e “descrever". O objetivo funcional da topografia é
levantar dados para fundamentar, sobretudo, serviços de construção civil e
mineração.
Há vários métodos para
determinar a área (A) do terreno delimitado pelos pontos fornecidos no
levantamento topográfico da questão. Pelo fato de os pontos em questão formarem
um polígono regular, o método mais simples consiste em localizar os pontos em
um plano cartesiano e desenhar o terreno. O resultado deste procedimento está
exposto na Figura 1.
Figura 1: Terreno formado
pelos pontos do problema.
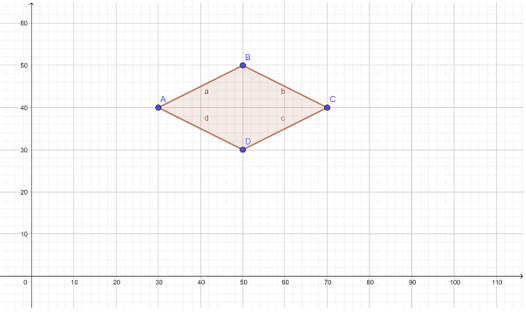
Observa-se que o
terreno é um losango constituído por 4 triângulos retângulos cuja base é igual
a 20 metros e a altura igual a 10 m. Lembrando que a área do triângulo é
igual ao produto entre a base a altura dividido por dois, calcula-se que:

Logo, a área do terreno
é de 400 m² e, portanto, a alternativa A está correta.
Gabarito do professor: Letra A.
A forma mais simples e rápida pra cálculo de poligonal.
- Monta uma tabela com as coordenadas X e Y, colocando o primeiro termo também na última linha;
- Multiplica cruzado da esquerda para a direita;
- Subtrai multiplicando da direita pra esquerda;
- Divide por 2;
- Valor sempre em módulo.
X | Y
30 | 40
50 | 50
70 | 40
50 | 30
30 | 40
A = [(30*50+50*40+70*30+50*40) - (40*50+50*70+40*50+30*30)] / 2
A = [(1500+2000+2100+2000) - (2000+3500+2000+900)] / 2= - 800 / 2 = - 400 = |400 m²|
Gab.: Letra A