O esquadro é para medir se a parede não está "tombando". É medido nas junções das paredes, onde forma 90º, sendo assim, utilizamos pitágoras.
Bom, foi marcado em um ponto A 1,5 m , e no ponto B 2,0 m. Essas medidas são os catetos, basta encontrarmos a hipotenusa:
h² = (1,5)² + (2,0)²
h²= 6,25
h= 2,5 m.
Gabarito: C
A questão trata do uso de esquadros na construção civil, o que
está diretamente relacionado à trigonometria do triângulo retângulo.
Para ilustrar melhor a situação colocada pela questão, ilustraremos as
dimensões utilizadas.
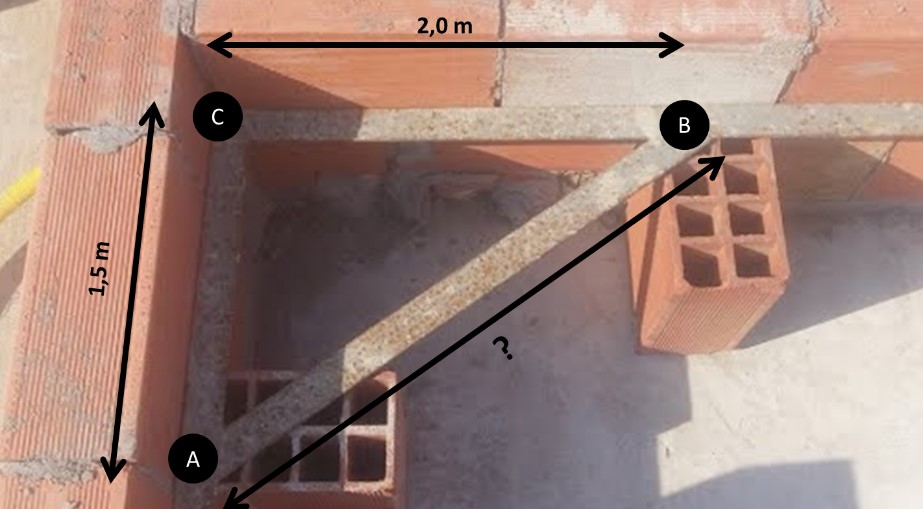
Inicialmente, o fiscal, partindo do vértice entre duas paredes, marcou a
distância 1,5m até o ponto A. Em seguida, 2,0m do vértice até o ponto B. Como a
questão envolve três pontos (ponto A, ponto B e vértice no encontro de
paredes), temos a formação e um triângulo que, neste caso, é um triângulo
retângulo, pois está definido a partir de um ângulo de 90º, no encontro das
paredes. Na trigonometria, chamamos esses lados medidos de catetos,
sendo o terceiro lado, definido entre A e B, denominado hipotenusa.
A partir disso, resolve-se a questão com aplicação do Teorema de Pitágoras,
no qual o quadrado da hipotenusa é igual à soma dos quadrados dos catetos, ou
seja:
AB²=AC²+BC²
Em que C é o
vértice formado no encontro de paredes.
Gabarito do Professor:
Alternativa C.