τ=M*ρ/J
τ - tensão (10MPa = 1,0kN/m²)
M- torque (VALOR PROCURADO)
ρ - distância do eixo de torção até a fibra mais externa do corpo de prova (50mm = 5cm)
J - momento polar de inércia (J = π.d^4 / 32)
M = τ*J/ρ = (1,0) * (π.10^4 / 32) / (5) = (1,0) * (981,25) / (5) = 196,25 kN.cm = 1,96kN.m
Primeiramente é importante
definir que a torção consiste no esforço com a tendência de torcer um
elemento em torno de seu eixo longitudinal. O principal exemplo de ocorrência são
as pontes, nas quais a torção é produzida por veículos e demais carregamentos
aplicados de forma assimétrica em relação ao centroide da seção transversal.
A tensão de
cisalhamento no eixo devido a um esforço torsão é calculado pela expressão
a seguir:
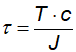
Em que τ é a tensão de
cisalhamento; T é o esforço torçor, também chamado de torque; c a distância
entre o centro do eixo e a fibra mais distante (no caso, c consiste no raio da
seção circular); e J o momento polar de inércia.
O torque máximo é obtido
ao isolarmos T na equação apresentada:
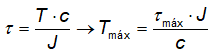
Visto isso e lembrando que
o momento polar de inércia de seções circulares é igual ao produto entre
π e o diâmetro (D) elevado a quarta potência dividido por 32, tem-se que:

Portanto, o valor do
torque atuante na extremidade livre da barra é de 1,96 kN·m. Assim, a
alternativa A está correta.
Gabarito do professor: Letra
A.