-
Como os eventos são independentes, a probabilidade pedida é a soma das probabilidades
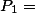João ser aprovado e Maria ser reprovada, 
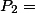João ser reprovado e Maria ser aprovada e 
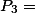os dois serem reprovados.
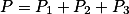
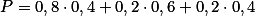
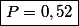. Letra D
-
Gabarito Letra D
P1 = Probabilidade de João ser reprovado é de 20% = 0,2
P2 = Probabilidade de Maria ser reprovada é de 40% = 0,4
P3 = Probabilidade de João e Maria serem reprovados juntos = 0,2 X 0,4 = 0,08
Qual é a probabilidade de que um ou outro seja reprovado?
A probabilidade do evento ocorrer é a probabilidade de João ser reprovado (0,2), MAIS a probabilidade de Maria ser reprovada (0,4), MENOS a probabilidade de Maria e João serem reprovados juntos (0,08).Portanto temos:
P = P1 + P2 - P3
P = 0,2 + 0,4 - 0,08
P = 0,52
-
Probabilidade de João e Maria serem reprovados (p1):
P1 = 0,2 * 0,4 = 0,08
Probabilidade de João ser aprovado e Maria ser reprovada (p2):
P2 = 0,8 * 0,4 = 0,32
Probabilidade de João ser reprovado e Maria ser aprovada (p3):
P3 = 0,2 * 0,6 = 0,12
Probabilidade de João e Maria serem aprovados (p4):
P4 = 0,8 * 0,6 = 0,48
Como a questão quer saber a chance de pelo menos um dos dois estar reprovado, calcular a soma de p1 + p2 + p3
0,08 + 0,32 + 0,12 = 0,52
-
Probabilidade de João e Maria serem aprovados:
PAprov= 0,8 * 0,6 = 0,48
Logo para 1 ; falta 0,52 que é a probabilidade de serem reprovados.
-
De acordo com o enunciado e considerando:
evento A: João ser reprovado.
evento B: Maria ser reprovada.
Tem-se as seguintes probabilidades (P):
P(A) = 20% = 0,2
P(B) = 40% = 0,4
Deseja-se saber a probabilidade da união dos dois eventos: P(A U B)
Relembrando as fórmulas, tem-se que:
P(A U B) =
P(A) + P(B) – P(A ∩ B)
P(A ∩ B) = P(A) x P(B) , quando os eventos forem independentes.
Assim,
P(A ∩ B) = 0,2 x 0,4 = 0,08
P(A U B) =
P(A) + P(B) – P(A ∩ B) = 0,2 + 0,4 - 0,08 = 0,52
Resposta D)
-
A disjunção somente será falsa quando houver dois resultados F.
Logo,
Probabilidade de João e Maria serem aprovados:
1 - (0,8 * 0,6) = 1 - 0,48 = 0,52
-
P(J) = 0,2
P(M) = 0,4
P(J∩M) = P(J) * P(M)
P = P(J) + P(M) - P(J∩M) = 0,52
-
P (A u B) = P (A) + P (B) - P (A ∩ B)
-
Dá pra resolver por tabela verdade...
P (joão) --- Q (maria) ----- P V Q
V V V
V F F
F V F
F F F
O valor que nos interessa é o que dá valor lógico F (são reprovados)
V joão = 8/10
FJoão = 2/10
V maria = 6/10
Fmaria = 4/10
fazendo as contas:
8/10*4/10 = 32/10
2/10*6/10 = 12/10
2/10*4/10 = 8/10
Somando as probabilidades: 52/100 = 0,52
-
P (A U B) = P (A) + P (B) - P (A ∩ B)
P(João U Maria) = P(João) + P(Maria) - P(João ∩ Maria)
P(João)=20/100=0,2
P(Maria)40/100=0,4
P(João ∩ Maria) 0,4x0,2=0,08
P(João U Maria)= 0,2 + 0,4 - 0,08
P(João U Maria)= 0,52
Gabarito:D
-
No caso de eventos independentes mutuamente exclusivos temos:
P(A) + P(B) – P(A ∩ B)
0,20+0,40-0,08=0,52 ou 52%
-
Ou um ou outro ou os dois reprovados.
JaMa -
JrMr - 0,2x0,4=0,08
JrMa - 0,2x0,6=0,12
JaMr - 0,8x0,4=0,32
0,08+0,12+0,32=0,52 ou 52%
-
P1: João reprovado: 20% = 0,2
P2: Maria reprovada: 40% = 0,4
P3: João e Maria reprovados: 0,2 x 0,4 = 0,08
P = P1 + P2 - P3
P = 0,2 + 0,4 - 0,08
P = 0,6 - 0,08
P = 0,52
-
Probabilidade (João reprovado E Maria não OU João não ser reprovado E Maria ser OU Joa reprovado E Maria reprovada)=
20% X 60% + 80% X 40% + 20% X 40% =
12% + 32% + 8% =
Probabilidade = 53% = 0.52
Outra solução seria:
100% - Probabilidade (João não ser reprovado E Maria não ser reprovada)
100% - (80% X 60%)
100% - 48% = 52% = 0.52
Fonte: Prof. Renato Oliveira.
https://www.youtube.com/watch?v=WkiZK-WYQnY
-
Prob. Complementar
Casos que não quero--> ambos serem aprovados:
---
P1 = Probabilidade de João ser reprovado é de 20% = 0,2---->Logo a chance de ser aprovado é 0,8
P2 = Probabilidade de Maria ser reprovada é de 40% = 0,4---->Logo a chance de ser aprovado é 0,6
--
1- (Maria e João serem Aprovados)
1-[ 0,8x0,6]
1-0,48
0,52