Esta questão sobre geometria
exige que o candidato atente para as propriedades geométricas do quadrado.
Sendo
assim, de acordo com o enunciado chega-se a figura abaixo:
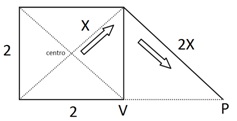
É importante que o candidato
perceba que a formiga anda na linha diagonal do quadrado até o primeiro
vértice. Posteriormente, após girar 90 graus ela anda por uma linha com a mesma
extensão da diagonal chegando assim ao ponto P. Sendo assim, a distância de V
até P é igual a 2, que corresponde ao valor do lado do quadrado.
(Resposta C)
Não vou conseguir resolver matematicamente por aqui. Mas vou tentar explicar de modo geral, só pra dar um "norte" para a resolução da questão, que pode ser resolvida com a expressão senx² + cosx² = 1, pois os deslocamentos da formiga mais a distancia que queremos descobrir formam um triangulo que não é um triangulo retângulo e por isso não pode ser resolvido pelo teorema de Pitágoras e sim com a expressão que passei.
Outras considerações pra facilitar:
A diagonal de um quadrado regular (lados iguais) de lado L é: L raiz de 2.
A formiga se desloca do centro até a um dos vértices (cantos), sendo assim, ela percorre o raio: (L raiz de 2)/2. Como L é 2, feito os cálculos, então o primeiro descolamento da formiga é raiz de 2.
Girando 90º, percorre uma distancia duas vezes maior do que percorreu anteriormente (que foi o raio): 2 x raiz de 2.
Do vértice mais próximo até o ponto P onde a formiga parou e mais os deslocamentos que ela percorreu, é formado um triangulo onde a hipotenusa é o maior descolamento da formiga 2 x raiz de 2; um dos catetos é o lado L do quadrado que é 2; e o outro cateto é o que queremos saber X.
Aplicada a primeira expressão, quem já estiver familiarizado com a aplicação de seno e coseno, vai descobrir que o resultado é exatamente 2, letra C.