-
Para atender à medida de segurança o quadrado deve estar, pelo menos, inscrito na circunferência.
Sabe-se que a diagonal do quadrado em relação ao seu lado, mede D=L (raiz de 2). Já que o quadrado está circunscrito, o raio da circinferencia é igual a metade da diagonal do quadrado, R = D/2, logo R=L(raiz de 2)/2. Multiplicando denominador e numerador por (raiz de 2), chega-se a R=L/ (raiz de 2).
Se o técnico resolver colocar uma base de raio maior, a medida de segurança continuará satizfeita, assim: R > ou = L/ (raiz de 2).
Alternativa "A"
-
Fazendo o esquema abaixo:
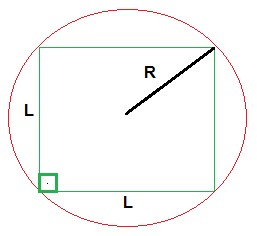
Assim, sabemos que para que a base quadrada seja fixada sobre a plataforma circular, o diâmetro do círculo deve ser maior ou igual à diagonal do quadrado de lado L, logo:
2L ≥ L√2 → L = R ≥ L√2/2, racionalizando: R ≥ L/√2
Resposta: Alternativa A.
-
Gente, alguém sabe me reponder porque não pode fazer a relação entre áreas?
-
pqp entendi mas buguei todo
-
2R = L x raiz 2
R = L x raiz 2/2 => R = L x raiz 4/2 x raiz 2 => R = L x 2/ 2 x raiz 2
R = L/raiz 2
Letra A
-
L=RxRAIZ2
L/RAIZ2=R
-
Outra alternativa, em vez de trabalhar 2R=L√2, é fazer por Pitágoras:
(2R)²=L²+L²
4R²=2L²
R²=L²/2
R=L/√2
-
gente o raio é a a diagonal do quadrado, só isso
r=d
d=L√2
então r=L√2 também
-
Diâmetro do círculo precisa ser igual ou maior que a diagonal do quadrado.
O raio de um círculo é o diâmetro dividido por 2. Portanto, o diâmetro do círculo é o raio multiplicado por 2.
2R ≥ L√2
R ≥ L√2/2
R ≥ L√2/2 * √2/2
R ≥ L * 2/2√2
R ≥ L/√2