-
se são 10 perguntas, e em cada pergunta ele tem 2 opções ( sim, nao) entao: 2^10
para aqueles que usam os tracinhos para cada evento
___ ___ ___ ____ ___ ___ ____ ___ ___ ___ no caso 1 traços para cada evento(pergunta)
2 . 2. 2 . 2 . 2 . 2 . 2 . 2 2 2 cada evento com duas opcoes(sim ou nao), entao multiplica 2 dez vezes = 1024
até agora calculados TODOS os possíveis casos que poderiam ocorrer. Pois a probabilidade se da com: número caso que satisfazem o que se pede dividido pelo total de casos possíveis
mas, agora ao inves de calcularmos, a os casos em que ele responde sim em pelo menos 1 das peguntas iria dar muito trabalho, então devemos calcular simplesmente o seu complemento, então caculariamos os casos em que ninguem responde sim. Só há um caso em que isto acontece quando todos os eventos são zero;
então fica P = 1 / 1024 ~= 0,0009
transformando em percentual:
P = 0,0009 x 100 = 0,09 %
se este é o percentual que não queria, entao 99,9% é o percentual que ele pede
-
O total de possibilidades é 2^10 = 1024. A única situação na qual não há resposta verdadeira é quando todas são falsas. Logo:
probabilidade de pelo menos uma resposta verdadeira: (1024-1)/1024 = 99,9%.
-
Pelo
enunciado, vemos que o total de possibilidades será de ois só temos duas possibilidades
de resposta (sim ou não a cada 10 perguntas feitas).
A única chance de não termos resposta verdadeira, seria quando todas forem falsas, assim, temos que calcular a probabilidade de pelo menos 1 resposta seja verdadeira:
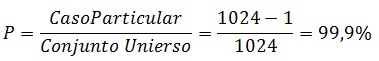
Logo a
resposta é Certo.
-
Fiz por probabilidade complementar. A probabilidade de se obter pelo menos uma resposta sim envolve fazer a P(uma sim) + P(duas sim) + P(três sim) ... e isso daria muito trabalho.
Para facilitar, fazemos 1-P(todas não), pois desta forma, estaríamos englobando os casos de "pelo menos uma sim".
=1-(1/1024)= 1-0,0009 = 0,9991 = 99,91%
-
GABARITO CORRETO faz-se pela propriedade complementar ou de negação, "pelo menos uma sim", tem-se como todas "não"
a probabilidade de todas "não" é: 1/2 elevado a 10, quando isso passa de 100 já dá menos de 1%!
-
Só um adendo: gente, se é a questão diz "a pelo menos uma pergunta", o complemento não é "todas não" (como todo mundo disse), mas nove respostas 'não', já que pelo menos uma tem que ser sim.
Isto dá maior que 99% também.
-
Nunca reclamei dos comentarios de nenhum professor aqui do QC,mas os do Prof. VINICIUS WERNECK deixam muito a desejar!
Mas tudo bem,ele deve partir do principio que comentário de PROFESSOR é mera formalidade,e todos aqui dominam o assunto.
-
A grande maoria reclama desse professor. Sou um desses... Ele pode ter um bom currículo, mas não é um bom professor, muito menos professor de concurseiro. Deixem seu 'NÃO GOSTEI' e o 'POR QUÊ' para o site melhorar seus serviços.
-
Você poderá responder SIM ou NÃO. Ou seja: 1/2 ou 1/2:
Sendo assim, você primeiro calcula a probabilidade de ocorrer o único evento que não pode, ou seja, TUDO NÃO!
1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 = 1 / 1024 ou seja, você teria 1 chance a cada 1024 de não ocorrer o evento desejado.
Logo, você possui 1023 chances de 1024 de ocorrer o evento que você deseja (SIM pra pelo menos uma), assim, você tem 1023 / 1024 = 99,9%
-
P(responder sim a pelo menos uma) = 1 - P(responder não a todas) =
1 - (1/1024) = 1023/1024 = 0,999
0,999 * 100 = 99,9%
CORRETO
-
vcs estdaram harvard?
-
binomio 4500/4096 = 0,01
-
Quando a questão pedir pelo menos , usa-se a fórmula: PELO MENOS UM= TOTAL - O QUE NÃO PODE.
TOTAL= 2x2x2x2x2x2x2x2x2x2, pois a cada pergunta haverá duas possibilidades, logo, multiplica-se tudo, resultando em 1024
O QUE NÃO PODE= que todas as respostas sejam ''não'', ou seja, a cada pergunta a pessoa só pode responder ''não'', como são 10 perguntas, fica da seguinte forma: 1x1x1x1x1x1x1x1x1x1= 1
pelo menos um = 1024 - 1 = 1023
1023/1024 é igual a 99,9% de possibilidades.
-
Comentário escrito em questão assim nao da!
-
Rapaziada, vamos pelo simples que da certo, se liguem:
Qual situação não me favorece?
Os participantes devem responder Sim ou não para 10 perguntas.
Para 1 pergunta, ele tem 2 possibilidade de resposta, vamos supor que ele tenha escolhido não para TODAS, teremos:
1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2 x 1/2= 1/1024
Podem aplicar agora o método da probabilidade complementar.
1) Pegue o denominador e subtraia o valor do numerador, ficará 1023.
2) Mantenha o denominador e coloque o valor encontrado no numerado, teremos:
1023/1024 = 99,9% > 99%
-
Galera, típico caso do cespe do "pelo menos um"
É interessante ter noção de como utilizar esse "pelo menos um" em todos os modelos de questões que o Cespe cobra.
"pelo menos um" = Total de possibilidades - o que eu n quero
"pelo menos um sim" -> pode sim 1 sim ou 2 sim ou 3 sim ou 4 sim (...)
Total = 2**10 -> 1024
O que eu n quero = que todos as respostas sejam "não"
1024/1024 - 1/1024 = 1023/1024 = 0,999 x 100% = 99,9%