-
É a negação que é equivalente:
~(pvq) <=> (~p) ^ (~q)
| P | Q | PVQ | ~(PVQ) | ~P | ~Q | (~P)^(~Q) |
| V | V | V | F | F | F | F |
| V | F | V | F | F | V | F |
| F | V | V | F | V | F | F |
| F | F | F | V | V | V | V |
-
A questão deveria ser anulada. Faltou a negação no enunciado.
-
Fiquei quebrando a cabeça aqui um tempão e me achando o burro por causa dessa questão... acredito em que esteja realmente passível de anulação!!!
-
Pessoal, trata-se de equivalência sim, uma vez que a negação da preposição tem o mesmo valor logico.
P ou Q= ¬(P ou Q), nega o primeiro e o segundo e troca o "ou" pelo "e", assim, fazendo a tabela verdade como feito pela colega, dará o mesmo valor lógico.
Espero ter ajudado!
-
A questão deve com certeza ser nula, pois nenhuma das alternativas são equivalentes...
Acredito que deve se tratar de um teorema de DE MORGAN que diz o seguinte:
~(p v q) eq. (~p ^ ~q)
~(p ^ q) eq. (~p v ~q)
-
O enunciado pede uma equivalência, mas a resposta apresenta uma negação.
-
Oii gente... não consigo entender de jeito nenhum essa questão, alguem me ajuda ai de uma forma mais clara por favor :S
-
Oii gente... não consigo entender de jeito nenhum essa questão, alguem me ajuda ai de uma forma mais clara por favor :S
-
A equivalência da disjunção (ou/v) é: " nega a primeira, conserva a segunda e troca o (ou/v) pelo se...,então (--->) = (~p-->q)", mas não tem essa resposta, no entanto, eu posso transformá-la numa conjunção (e/^). Primeiro: " conserva a primeira, nega a segunda e troca o se...,então(--->) pelo (e/^)=(~p^~q)". Resposta letra D.
-
Nesta questão, o enunciado deveria ter dito “pode-se afirmar
que a NEGAÇÃO da disjunção...”, uma vez entendido isso, vamos fazer a tabela
para p v q
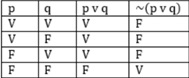
Agora vamos fazer a tabela verdade para cada um
a) ~pv ~q
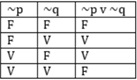
b) ~ pvq

c) p^~q

d) ~p^~q
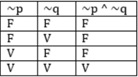
Logo, vemos que a única
alternativa possível é a letra D.
-
Muita gente confundindo equivalência com negação... Cuidado!
-
Poxa vida! Um examinador não saber o conceito do básico da lógica proposicional é o fim do mundo. Me ajuda aí!
Que coisa medíocre essa.
Deveriam demitir um funcionário desses por ineficiência no serviço.
-
Equivalência:
p v q <=> q v p .............. p v q = ~p ^ ~q (negação).
-
Ele não pede a negação e sim a equivalência, o que não é a mesma coisa. P v Q significa dizer que PELO MENOS UMA DAS DUAS PRECISA OCORRER! Então, ou ocorre P ou ocorre Q ou ocorrem as duas ao mesmo tempo. Portanto, como equivalência, a alternativa seria a letra C (P ^ ~Q) pois esta alternativa está deixando claro que Q não ocorre e como é preciso que ocorra pelo menos uma das duas, então se Q não ocorre, P precisa ocorrer! ;)
-
Ivisson Moraes
Na verdade, fazendo a tabela verdade não consegui encontrar gabarito nessa questão, seria a letra D se ao invés de dizer equivalência, a banca falasse em negação
-
seria a negação de p v q que é igual ~p ^ ~q
-
ela fala em equivalencia ou negacao?????????????????
-
Letra D seria negação de P v Q. As equivalências seriam: Q v P ou com a condicional ~ P-->Q.
-
Equivalente? Nenhuma das respostas.
-
Equivale = <=>
VAMOS LÁ!
p v q <=> ~p -> q (se não encontrou tente O Modus Tollens. Outra forma de equivalência que só pode ser feita no ->).
~p -> q <=> ~q -> p ( No Modus Tollens inverte as proposições negando, permanecendo o mesmo conectivo).
Mesmo assim não obtivemos o resultado.
Transformando novamente: ~q -> p <=> q v p
Novamente: q v p <=> ~q -> p.
Voltamos, vamos tentar Modus Tollens: ~q -> p <=> ~p -> q
PERCEBAM QUE VOLTAMOS A ESTACA ZERO.
Nenhuma das possíveis respostas existem: ~p -> q, ~q -> p, q v p.
-
A equivalência do conectivo v, se obtém transformando-o em uma -> :
p v q <=> ~p -> q
Como não obtvemos, façamos O Modus Tollens a partir dessa -> :
~p -> q <=> ~q -> p
Não existe resposta.
Além da letra d ser a negação da proposição em questão, nada tem haver o conectivo ^ com equivalência.
-
Essa questão foi anulada de acordo com o gabarito final. FONTE: http://www2.ibfc.org.br/arquivos/hubpos/GABARITO_IBFC_201_POS%20RECURSO.pdf
-
Acho que a resposta é letra B (~p v q) Nega a primeira + disjunção (ou) + mantém a segunda!
Alguém sabe o argumento da anulação?
-
Acredito que seja letra "d)",
p v q = ~p ^ ~q
não tenho certeza... Qual o motivo da anulação? Alguma das respostas é correta?
-
A equivalência da Disjunção OU é: ~P então Q.
Ex: Paulo é Sergipe ou Cesar é Confiança. Logo, equivale: Se Paulo não é Sergipe então Cesar é Confiança.
-
Pessoal não tenham duvida que a resposta é b. Eles anularam pq faltou no enunciado dizer que v e disfunção. O Cespe sempre informa.
-
a letra A não seria contrapositiva ja que não tem a opção de PvQ = QvP?
Podendo assim aplicar a forma de equivalencia do -->
-
Questão anulada, a resposta deveria ser "~P -> Q"
-
VIM DO FUTURO PARA DIZER QUE ESTAMOS INDO PARA ABRIL, E NEM 10% DA POPULAÇÃO BRASILEIRA FOI VACINADA COM A PRIMEIRA DOSE, GRAÇAS À GESTÃO DE QUALIDADE DO ATUAL GOVERNO.