-
Essa questão se encontra detalhada e muito bem explicada pelo professor Arthur no link abaixo:
http://d3pt2alc3jyv7g.cloudfront.net/46002/00000000000/curso-4519-aula-00-v1.pdf?Expires=1402526161&Signature=O-Ekk-YcmeFIncQUT7eGKmJkoetjOG4k8Y8o~k8kohQP3aVD1Tnp7SN5er3at2qF1NClgN-9msnLmgcP1ZxQDuPupLj5B6Oyp-cTok0qSJoQbCJxdxPTtnCi~tVnljDgCxBzyf4hPn8fuONCb1JUKjDESh2PtFWd7AU1vfnwNro_&Key-Pair-Id=APKAIKHUAVWTIL5FVANA
-
M = c . (1 + it) = c + cit
Juros = cit
J1 + J2 = ?
(1) 15.660 = c + 10ci (2) 32.480 = 2c + 30ci
J1 = 10ci J2 = 30ci
Juros1 + Juros2 = 10ci + 30ci = 40ci
32.480 = 2c + 30ci (dividir por 2)
16.240 = c + 15ci (diminuir a equação "1")
- (15.660 = c + 10ci)
580 = 5ci
J1 + J2 = 40ci, para 5ci virar 40ci é preciso multiplicar por 8. Assim:
4.640 = 40ci
J1 + J2 = 40ci = 4.640
Gabarito letra C.
-
Indira,
O link abaixo não está funcionando, poderia postar a explicação no comentário?
Grato.
-
oi...
Primeira aplicação:
Segunda aplicação:
Dividindo as duas equações:
Simplificando 2 com 32.480:
Simplificando numerador e denominador (dividindo ambos por 20):
Multiplicando cruzado:
Voltando em I, calculamos o valor do capital:
O capital da segunda aplicação é o dobro disso:
A soma dos capitais é:
A soma dos montantes é:
A diferença entre os dois valores nos dá a soma dos juros:
Gabarito: C
Segunda solução: mais rápida
Primeira aplicação: capital C, durante 10 meses, gerando montante de 15.660
Segunda aplicação: capital 2C, durante 15 meses, gerando montante de 32.480
Se a segunda aplicação fosse de C reais (metade do valor original), o montante também seria reduzido pela metade. O montante seria de
Assim, se tivéssemos duas aplicações de C reais, uma por 10 meses e outra por 15 meses, os montantes seriam 15.660 e 16.240.
A diferença entre eles corresponde justamente ao juro conseguido durante o período de 5 meses, que é a diferença de prazo entre as aplicações. Assim, o juro para 5 meses corresponde a:
Com isso, acabamos de descobrir que o juro correspondente a uma aplicação de 5 meses do capital C é de R$ 580,00.
Na aplicação 1, tivemos 10 meses (10 meses é o dobro de 5 meses). Logo, o juro será de duas vezes 580:
Esse é o juro da primeira aplicação.
Na aplicação 2, tivemos 15 meses (15 meses é o triplo de 5 meses). Logo, o juro será de três vezes 580:
Lembrem-se ainda de que, na aplicação 2, o capital na verdade é 2C. Então o juro tem que ser dobrado:
O juro total fica:
http://exatasparaconcursos.wordpress.com/2014/01/22/resoluo-da-prova-de-matemtica-financeiraicms-rj-2014/
estava nesse site na resolução de matematica financeira do icms rj. Realmente não sei porque não está entrando pela resolução do professor artur, mas veja desta forma. Duas formas de resolver.
Se quiser uma explicação melhor posso passar depois, desculpe o ctrl c + cltr v.
Bons estudos.
-
J1 = C1 x i x n1 J2 = C2 x i x n2
J1 = C x i x 10 j2 = 2C x i x 15
J1 = 10xC x i J2 = 30 x C x i
se C1 = M1-J1 se 2C = M2-J2
então: J1 = (M1-C) Então: J2 =(M2-2C)
(15.660-C) = 10Ci (32.480-2C) = 30Ci
15.660 = 10Ci+C 32.480=30Ci+2C
10Ci+C = 15.660 30Ci+2C = 32.480
Colocando o C em evidência
C(10i+1) = 15.660 2C(15i+C)=32.480
C=15.660/(10+i) C = 32.480/2(15i+c)
C = 15.660/(10i+1) C = 16.240/(15i+1)
Então
15.660/(10i+1) = 16.240(15i+1)
(15i+1)/(10i+1) = 16.240/15.660 =1,037
15i+1 = 1,037(10i+1) = 10,37i + 1,037
15i+1 = 10,37i+1,037
15i-10,37i = 1,037-1
4,63i = 0,037
i=0,037/4,63 = 0,0080 = 0,80% ao mês.
A partir dessa informação é possível encotnrar o capital:
C = 15.660/(10i+1) = 15.660/(10 x 0,008+1) = 14.500,00
ou pela fórmula da segunda aplicação:
C = 16.240/(15i+1) = 16.240/(15 x 0,008 +1) = 14.500,00
A partir daí é possível encontrar os juros de cada aplicação e a soma desses juros:
J1 + J2 = ?
14.500 x 0,80% x 10 + 29.000 x 0,80% x 15 = 4.640,00 Letra c.
-
Resolução de todas as questões de matemática Icms RJ 2014 pelo professor Arthur Lima, do Estratégia:
https://d3pt2alc3jyv7g.cloudfront.net/46002/00000000000/curso-4519-aula-00-v1.pdf?Expires=1413915873&Signature=A7qyYlZrWXkc~SnJyIRdCCZUwQxmIm-2UhYwfELoEJB64XukF3Pb4lwzwqVVkdBXzYv~1D86Sv7LSsIXE9MrTE3joC~xxDwUZFwPlWRqBfnuEVwimuWbUHKaG87r~SUeL0PkW7V85G5SYWhmbMBiiJANQv4s47jIGPhrPUVYMWI_&Key-Pair-Id=APKAIKHUAVWTIL5FVANA
-
"32.480 = 2c + 30ci (dividir por 2)
16.240 = c + 15ci (diminuir a equação "1")
- (15.660 = c + 10ci)
580 = 5ci"
Na explicação da Lilian eu não entendi o pp de dividir a equação por 2?
-
Falta explicações em videos para essa disciplina, custa mais quanto na mensalidade para providenciar isso? Tirem um pouco de video de portugues e coloquem o esforço um pouco para mat. financeira
-
Primeira aplicação:
M1=C1 x (1+in1)
15.660=C x (1+10i) (I)
Segunda aplicação:
M2=C2 x (1+in2)
32.480=(2C) x (1+15i) (II)
Dividindo as duas equações:
32.480=(2C) x (1+15i)
15.660=C x (1+10i)
Corta-se o C:
32.480=2 x (1+15i)
15.660= (1+10i)
Simplificando 32.480 com 2:
16.240=(1+15i)
15.660= (1+10i)
Simplificando numerador e denominador (dividindo ambos por 20):
812=(1+15i)
783= (1+10i)
Multiplicando cruzado:
812 x (1+10i) = 783 x (1+15i)
812+8.120i = 783+11.745i
11.745i-8120i = 812 - 783
3.625i = 29
i = 29 / 3.625
i=0,8%
Voltando em (I), calculamos o valor do capital:
15.660 = C x (1+10i)
15.660 = C x (1+10x0,008)
15.660 = C x (1,08)
C = 15.660 / 1,08
C = 14.500
O capital da segunda aplicação é o dobro disso:
C2 = 2C
C2 = 14.500 x 2
C2 = 29.000
A soma dos capitais é:
14.500 + 29.000 = 43.500
A soma dos montantes, que o enunciado já deu, é:
32.480 + 15.660 = 48.140
A diferença entre os dois valores, nos dá a soma dos juros:
48.140 - 43.500 = 4.640 => J1+J2
Gabarito: C
___________________________________________________________________________________________________
Segunda solução: mais rápida
Primeira aplicação: capital C, durante 10 meses, gerando montante de 15.660
Segunda aplicação: capital 2C, durante 15 meses, gerando montante de 32.480
Se a segunda aplicação fosse de C reais (metade do valor original), o montante também seria reduzido pela metade. O montante seria de 32.480 / 2 = 16.240
Assim, se tivéssemos duas aplicações de C reais, uma por 10 meses e outra por 15 meses, os montantes seriam 15.660 e 16.240.
A diferença entre eles corresponde justamente ao juro conseguido durante o período de 5 meses, que é a diferença de prazo entre as aplicações. Assim, o juro para 5 meses corresponde a:
16.240 - 15.660 = 580
Com isso, acabamos de descobrir que o juro correspondente a uma aplicação de 5 meses do capital C é de R$ 580,00.
Na aplicação 1, tivemos 10 meses (10 meses é o dobro de 5 meses). Logo, o juro será de duas vezes 580:
2 x 580 = 1.160 => Esse é o juro da primeira aplicação.
Na aplicação 2, tivemos 15 meses (15 meses é o triplo de 5 meses). Logo, o juro será de três vezes 580:
3 x 580= 1.740
Lembrem-se ainda de que, na segunda aplicação, o capital na verdade é 2C. Então o juro tem que ser dobrado:
2 x 1.740 = 3.480=>Esse é o juro da segunda aplicação.
O juro total fica:
3.480 + 1.160 = 4.640
Vejam como esta segunda resolução praticamente não exige contas.
__________________________________________________________________________________________
FONTE: https://goo.gl/JeHPcq
-
Dados da questão:
Primeira capitalização:
M1= 15.660
t= 10 meses
i= ?
C1=?
Segunda capitalização:
M2 = 32.480
t=15 meses
i=?
C2 = 2*C1
J1+J2. =?
Começamos pelo montante1:
M 1 =C1 *(1+t1i)
15.660 = C*(1+10i) (1)
Depois, o montante 2
M2 = C2 *(1+t2i)
32.480 = (2C)*(1+15i)
(2)
Dividimos a equação 2 pela 1:
32.480/15.660 =2C*(1+15i)/C*(1+10i)
16.240/15.660 =(1+15i)/(1+10i)
812/783 =(1+15i)/(1+10i)
812 + 8120i = 783 +11.745i
I=(11745-8120)=812-783
3625i=29
i=29/3625
i= 0,008
C1=15.660/(1+10i)
C1=15.660/(1+10 x 0,008)
C1= 14.500
C2=16240/(1+15i)
C2=16.240/(1+15 x 0,008)
C2= 2*14.500,0
C2=29.000
Se M1= 15.660 e M2 = 32.480, então os
valores dos juros são:
Juros1= M1 - C1 = 15.660-14.500= 1.160
Juros2= = M2 – C2 = 32.480-29.000= 3.480
J1+ J2 =1.160 + 3.480
Gabarito: Letra “C"
-
bom dia galera. prefiro resolver por sistema. é mais rápido.
M1=c(1+in)
M2=2c(1+in)
32480=2c(1+i15)
15660=c(1+i10)
multiplico as equações e a 2ª equação, multiplico por -2 para eliminar a incógnita
32480=2c+30ci
(15660=c + 10ci)*-2
agora somo as equações
32480=2c+30ci
+
-31320=-2c - 20ci
=1160=10ci
j1=10ci
j1=1160
j2=2*15*ci
j2=30ci
j2=3480
j1+j2=1160+3480=
4640
resolvi em 2 minutos e 30 segundos
obrigado pelos aplausos
-
De que lugar saiu esse 15?
-
Solução: mais rápida
Primeira aplicação: capital C, durante 10 meses, gerando montante de 15.660
Segunda aplicação: capital 2C, durante 15 meses, gerando montante de 32.480
Se a segunda aplicação fosse de C reais (metade do valor original), o montante também seria reduzido pela metade. O montante seria de
32.480 / 2 = 16240
Assim, se tivéssemos duas aplicações de C reais, uma por 10 meses e outra por 15 meses, os montantes seriam 15.660 e 16.240.
A diferença entre eles corresponde justamente ao juro conseguido durante o período de 5 meses, que é a diferença de prazo entre as aplicações. Assim, o juro para 5 meses corresponde a:
16240 - 15.660 = 580
Com isso, acabamos de descobrir que o juro correspondente a uma aplicação de 5 meses do capital C é de R$ 580,00.
Na aplicação 1, tivemos 10 meses (10 meses é o dobro de 5 meses). Logo, o juro será de duas vezes 580:
2 x 580
Esse é o juro da primeira aplicação.
Na aplicação 2, tivemos 15 meses (15 meses é o triplo de 5 meses). Logo, o juro será de três vezes 580:
3 x 580
Lembrem-se ainda de que, na aplicação 2, o capital na verdade é 2C. Então o juro tem que ser dobrado:
2 x 3 x 580 = 6 x 580
O juro total fica:
2 x 580 + 6 x 580 = 8 x 580 = 4.640
-
PRECISAMOS CORRECOES EM VIDEO PELOS PROFESSORES DA Q CONCURSO!!!
PRECISAMOS TBEM DE AULA, NE???
-
Elizandra Campo, excelente explicação! obrigado
-
percebam que os juros por mês é de 116 reais, afinal
32480= 2C*(1 + 15i)
divide 32480/2=16240
16240= C*(1+ 15i) ====> SEGUNDA EQUAÇÃO SIMPLIFICADA
Os juros da primeira equação são 15660, sobre um capital 1C aplicados por 10 meses.
Então sabemos que 16240 (juros sobre um capital 1C aplicados por 15 meses) menos os juros sobre o capital 1C por 10 meses= 580 rendendo por 5 meses sobre um capital C.
Basta multiplicar por 2 e teremos o valor de juros sobre capital 1 C para 10 meses = 1160
Contudo o outro capital foi 2C. Então tem que pegar 580 multiplicar por 3 (5meses X 3= 15 MESES) e então multiplicar esse valor por 2, porque rendeu sobre um capital 2C.
Total:1160 + 3480=4640.
-
Não era mais fácil resolver assim:
32480 - 15660 = 16820
16820 - 15660 = 1160 encontramos os juros de um total de 5 meses, agora falta os outros 20 meses, pois era 10 meses na primeira aplicação e 15 meses na segunda. Então encontramos a diferença de 5 meses entre 15 e 10 meses. Agora calculamos 1160*4 meses = 4640
Certo ou Errado?
-
1) C , t=10m, M= 15.600, i
2) 2C, t=15m, M= 32.480, i
1) 15660 = C*(1+10i) .: 15660 = C + 10iC
2) 32480 = 2C (1+15i) .: 32480 = 2C + 30i .: 16240 = C + 15iC MULTIPLICA POR (-1)
16240 = C + 15iC
-15660 = -C - 10iC
580= 5iC
iC=116
SUBSTITUINDO:
15660 = C+1160
C=14500
15660 = 14500 + 10 * 14500i
1160= 10*14500i
116=14500i
i = 0,8% a.MÊS!
Usando a fórmula J= C*i*t, descobre-se que:
J1= 1160 e J2 =3480
Somando-se: 1160+3480 = 4640
-
Seja P o valor do primeiro capital. Logo, o segundo capital é igual a 2P (pois é o dobro do primeiro). Na fórmula de juros simples, temos:
M = C x (1 + j x t)
Para a primeira aplicação, temos montante M = 15.660,00 e prazo t = 10 meses, portanto:
15.660 = P x (1 + j x 10)
Na segunda aplicação temos M = 32.480,00 e t = 15 meses. A taxa de juros é a mesma (j), e o capital inicial é o dobro do primeiro (2P). Assim,
32.480 = 2P x (1 + j x 15)
Na primeira equação obtida, podemos isolar a variável P, ficando com:
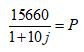
Substituindo P pela expressão acima, na segunda equação, temos:

32480 + 324800j = 31320 + 469800j
32480 – 31320 = 469800j – 324800j
1160 = 145000j
j = 0,008
j = 0,8%
Com isso podemos obter o valor do capital P:

P = 14500 reais
O capital da segunda aplicação é o dobro (2P), ou seja, 29000 reais. Podemos agora calcular os juros obtidos em cada uma das aplicações, lembrando que a fórmula J = C x j x t relaciona os juros obtidos com o capital aplicado (C), a taxa de juros (j) e o prazo da aplicação (t):
J = 14500 x 0,008 x 10 = 1160 reais
J = 29000 x 0,008 x 15 = 3480 reais
Portanto, a soma dos juros é igual a 1160 + 3480 = 4640 reais.
Resposta: C