-
Sabemos que o volume será a área da base x altura.
Para encontrar a altura, basta dividir o octógono em oito triângulos isósceles cujo lado maior é igual ao raio (R) da circunferência. No centro, teremos um ângulo de 45 graus (360 da circunferência divido por 8 triângulos = 45 )
Para encontrar a área de cada triângulo usaremos A = (a.b.sen 45)/2, assim A =( 7.7.sen 45)/2
Área total = 8 x área de cada triângulo = 98 raiz de 2.
Volume = 98 raiz de 2 x 13
=1783,6
-
Acompanhem comigo fazendo os desenhos e contas no papel:
O volume do prisma é:
V = (Área_da_base)*altura
A altura vale 13 cm, conforme dado no enunciado.
A área da base é a do octógono regular.
Se você, como eu, não sabe a fórmula, podemos deduzi-la rapidamente. A maneira mais fácil é dividir o octógono em 8 triângulos isósceles de lados R, R e L, onde R é o raio da circunferência na qual o octógono está inscrito e L o valor do lado do octógono.
É fácil descobrir que o ângulo entre os lados R e R desse triângulo vale 360º/8 = 45º.
A área desse triângulo vale:
A' = (Área_da_base)*altura/2 = L*h/2
Não sabemos o valor de L nem de h, mas podemos descobrir.
Considerando L a base desse triângulo, sua altura dividirá esse ângulo de 45º em dois ângulos de 22,5º.
Usando as definições de seno e cosseno, temos:
sen(22,5º) = (L/2)/R = L/(2*R)
cos(22,5º) = h/R
Reorganizando essas equações:
L = 2*R*sen(22,5º)
h = R*cos(22,5º)
Logo,
A' = L*h/2 = 2*R*R*sen(22,5º)*cos(22,5º)/2 = R² * sen(22,5º)*cos(22,5º)
Chegamos a um ponto crítico, pois não sabemos os valores de seno e cosseno de 22,5º. Agora é necessário saber que:
sen(a+b) = sen(a)*cos(b) + sen(b)*cos(a)
(OBS.: Macete para lembrar da fórmula: decorar o poeminha:
"Minha terra tem palmeiras
onde canta o sabiá,
seno A cosseno B,
seno B cosseno A")
E ter um pouco de perspicácia para ver que se fizermos b = a, temos que:
sen(2*a) = 2*sen(a)*cos(a), logo:
sen(22,5º)*cos(22,5º) = sen(45º)/2
Substituindo na fórmula da área do triângulo:
A' = R² *sen(45º)/2
A área do octógono é a soma das áreas desses 8 triângulos, e vale:
A'' = 8*A' = 8*R² *sen(45º)/2 = 4*R² *sen(45º) => essa é a fórmula da área do octógono regular inscrito numa circunferência de raio R!!
Logo, o volume do prisma será:
V = A'' * 13 = 13*4*R² *sen(45º)
Já sabemos que sen(45º) = (Raiz_de_2)/2 = 1,4/2 e R = 7 cm, então
V = 13*4*7*7*1,4/2 = 1783,6 cm³
Gabarito: C
-
Sabe-se que o volume é dado pela área da base vezes altura:
V = 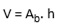
Pelo enunciado, temos de base um octógono regular e altura 13cm. Então:
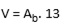
A
área de um octógono regular inscrito numa circunferência de rio r, é
igual a 8 vezes a área de um triângulo isósceles de lados r, assim:
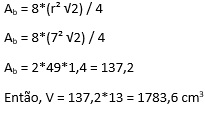
Letra C.
-
Sb - área do octógono -> Sb = 8 . a² V2 / 4
raio = a (aresta)
a = 7
H - altura
V - Volume -> V = Sb . H
Solução
Sb = 8 . 7² V2 / 4
Sb = 117,6
V = 117,6 . 13
V= 1783,6
-
Sb - área do octógono -> Sb = 8 . a² V2 / 4
raio = a (aresta)
a = 7
H - altura
V - Volume -> V = Sb . H
Solução
Sb = 8 . 7² V2 / 4
Sb = 117,6
V = 117,6 . 13
V= 1783,6
-
Sb - área do octógono -> Sb = 8 . a² V2 / 4
raio = a (aresta)
a = 7
H - altura
V - Volume -> V = Sb . H
Solução
Sb = 8 . 7² V2 / 4
Sb = 117,6
V = 117,6 . 13
V= 1783,6
-
Sb - área do octógono -> Sb = 8 . a² V2 / 4
raio = a (aresta)
a = 7
H - altura
V - Volume -> V = Sb . H
Solução
Sb = 8 . 7² V2 / 4
Sb = 117,6
V = 117,6 . 13
V= 1783,6
-
as respostas são bem distantes. resolvi em 30 segundos fazendo a área do círculo e sabendo que seria um pouco maior que o normal.