CERTA
1º passo) Inicie a resolução da questão com um Diagrama de Venn. Comece
sempre pela interseção que abrange o maior número de elementos. No caso, a
própria questão informa que 20 turistas visitaram todos os três pontos
turísticos, ou seja: PF ∩ TJA ∩ CM = 20. A questão também informar que 30
visitaram apenas a PF. Daí por diante é só completar as demais interseções,
lembrando-se de subtrair os 20 visitantes que são comuns aos três:
Apenas PF=30
CM ∩ TJA= 30 (50 – 20)
PF ∩ CM=5 (25 – 20)
PF ∩ TJA=15 (70-30-5-20)
Apenas TJA=15 (80-30-20-15)
Apenas CM=15 (70-5-20-30)
Com o Diagrama pronto, descobrimos que há ao todo 130 turistas: 30+15+20+5+30+15+15=130
ATENÇÃO: Não tente somar 70+80+70 ou dará errado. Parece bobo isso, mas essa
é a nossa tendência...
2º passo) Resolva a probabilidade: número de casos possíveis / número de
casos totais = 20/130= 0,15%
0,15% > 0,14%, portanto CORRETA
Obs.: as respostas do Cespe são, geralmente, números aproximados. Então, se
a sua resposta ficou muito diferente, refaça as contas, pois deve ter errado
algo.
Fazendo o diagrama de Venn para sabermos quantos turistas faziam parte deste grupo:
Obs: Para construir o diagrama, deve-se começar pelo centro, ou seja, pela interseção dos três conjuntos. Logo depois temos que subtrair os elementos conforme o diagrama a baixo, para evitar que contemos o mesmo elemento outra vez.
"70 turistas visitaram a PF", quando o enunciado diz isso, ao completarmos o diagrama, percebe-se que esse quantitativo, faz parte da interseção entre PF e TJA.
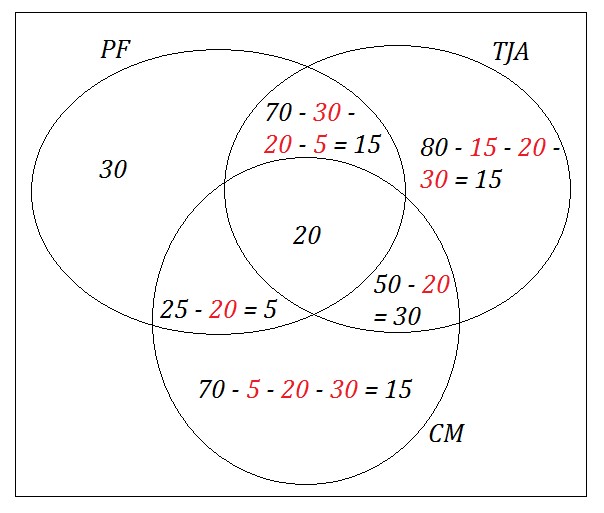
Somado tudo: 30 + 15 + 15 + 30 + 15 + 5 + 20 = 130 turistas, esse número também é o nosso espaço amostral, assim:
P = 20 / 130
P ≅ 0,15
Resposta: Certo