-
Resposta certa que é a alternativa D
MÉTODO DAS PREMISSAS VERDADEIRAS: Encontrar
uma premissa simples ou uma conjunção (^), julgar todas as
premissas verdadeiras, caso a conclusão seja verdadeira o argumento é
válido, caso a conclusão seja falsa o argumento é inválido.
Testei com esse
método as alternativas A, B e C até chegar à resposta certa que é a alternativa D. Vamos à certa:
P1: A →
B
P2: C
→ D
P3: D ^
A
_____________
C: B v
C
Inicia-se
valorando a P3, que é conjunção, considerando as duas proposições verdadeiras;
Logo, na P1
A é verdadeira e verdadeiro anda para frente, então B também é verdadeira;
Na P2 já foi
valorado D que é verdadeira e sendo condicional é garantia de que a P2 é
verdadeira, mesmo sem conseguir valorar C;
Na
conclusão, pode-se garantir que B é verdadeira e consequentemente a conclusão
também, já que a única maneira de ser falso seria ambas as proposições fossem falsas.
Caso
persistam dúvidas, pode ser resolvido pelo MÉTODO DA CONCLUSÃO FALSA: encontrar
na conclusão uma proposição
simples, disjunção(v) ou condicional (→) e julgar como falso, julgar
premissas verdadeiras, caso sejam verdadeiras o argumento é inválido,
caso pelo menos seja falsa o argumento é válido.
Nesse caso
só poderia ser testada a letra D que é a única com disjunção.
P1: A →
B
P2: C
→ D
P3: D ^
A
_____________
C: B v
C
Inicia-se
valorando a conclusão como falsa, logo as proposições B e C são falsas;
Na P1 B é falsa,
e falso anda para trás. Sendo assim A também é falsa;
Na P2 C é
falsa, então não se pode valorar D;
Na P3 D é
falsa, então já existe a garantia de que a P3 é falsa, pois a única maneira de
ser verdadeira é se ambas as proposições fossem verdadeiras.
Com a
conclusão falsa e pelo menos uma premissa falsa o argumento é Válido.
Ou ainda pelo MÉTODO
DA TABELA VERDADE: desenhar toda a tabela, olhar apenas as linhas das premissas onde elas sejam todas verdadeiras,
caso a conclusão nestas linhas também
seja verdadeira o argumento será válido, caso pelo menos uma seja falsa o
argumento é inválido.
ABCD A→B C→D D^A BvC
VVVV V V V V
VVVF V F F V
VVFV V V V V
VVFF V V F V
VFVV F V V V
VFVF F F F V
VFFV F V V F
VFFF F V F F
FVVV V V F V
FVVF V F F V
FVFV V V F V
FVFF V V F V
FFVV V V F V
FFVF V F F V
FFFV V V F F
FFFF V V F F
-
A regra é ter todas as premissas como verdadeiras... Então vocẽ as olha atentamente e percebe
Para a premissa I ser verdade(lembrando que somente será falsa se tivermos V-->F = F) podemos ter:
Carlos é legista é médico
V ---------> V = V
F ---------> V = V
F ---------> F = V
Então veja, temos várias opções para a premissa ser verdadeira e a mesma coisa vale para a premissa II. Então olhamos para a premissa III em que, pela regra, só será verdadeira caso ambos sejam verdade:
Ana é policial civil e Carlos é legista.
V e V = V
Agora, tendo a certeza nos argumentos, "voltamos" para as outras premissas e concluímos:
I. Se Carlos é legista, então ele é médico. ( V na frente, obrigatoriamente não podemos ter o F depois, V-->F = F)
V ---------> V = V
II.Se Ana é perita criminal, então ela é policial civil. (Ana ser perita contraria o que descobrimos na premissa III)
F ------------> V = V
Então, dadas as opções, a única correta é a letra D.
-
A ideia é simples... :D 1º passo: considere a conclusão falsa e as premissas verdadeiras (lembrando que: para a ''disjunção'' ser falsa devemos negar as duas proposições); 2º passo: se não houver contradição, então o argumento é, realmente, inválido; 3º passo: havendo contradição, ou seja, pelo menos uma premissa falsa, então o argumento será válido, e foi isso que aconteceu na ''terceira'' premissa da questão. espero ter ajudado ;)
-
Vamos verificar a validade do
argumento aplicando a tabela verdade, que pode ser aplicada em qualquer
situação, desde que preferencialmente o argumento tenha no máximo duas proposições
simples.
Arrumando as ideias:
A: Carlos é
legista (V)
B: Carlos é
médico (V)
C: Ana é
perita criminal (V)
D: Ana é
policial civil (V)
Como temos 4 variáveis (A, B, C, D),
vamos seguir a seguinte lógica para construir a nossa tabela verdade:
1)
A quantidade de combinações possíveis
sempre ser 2n, onde n é o número de variáveis.
2)
Para construir a tabela com 4 variáveis:
2.a)
Descubra quantas linhas teremos: 24
= 16.
2.b)
Comece com a coluna da direita (última variável) e alterne, em cada uma das 16 linhas, os valores V e
F
2.c)
para a penúltima variável, alterne 2 "V" e 2 "F" para as 16
linhas
2.d)
para a antepenúltima, alterne 4 "V" e 4
"F" e assim por diante.
Assim, uma vez construída a tabela
verdade para 4 variáveis, a regra da tabela verdade nos diz para olhar apenas as linhas das premissas onde elas
sejam todas verdadeiras, caso a conclusão nestas linhas também seja verdadeira
o argumento será válido, caso pelo menos uma seja falsa o argumento é inválido.
Então:
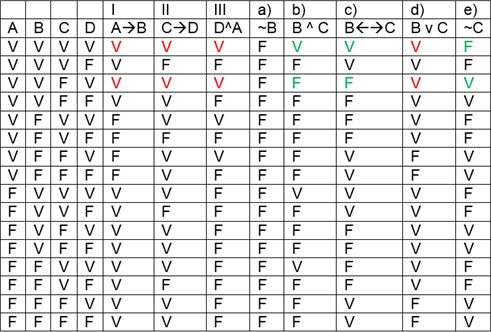
Finalmente, observando a tabela
verdade, a única alternativa que apresenta uma conclusão que pode ser indicada
para que, juntamente com essas três premissas, se tenha um argumento válido é letra D.
-
Demorei, mas entendi.
Para que a premissa III seja verdadeira, o valor de ambas as preposições (Ana é policial civil E Carlos é legista) deverá ser verdadeiro (V ^V= V)
A partir daí, se descobre na premissa II que a preposição "Carlos é médico" é verdadeira, porque não poderá ser falsa para que a condicional seja verdadeira.
Na premissa II, fica impossível se afirmar o valor de "Ana é perita criminal", pois essa preposição pode ser tanto F quanto V para que a condicional seja verdadeira.
Assim, a única alternativa que dará certeza de que o argumento será válido será a D, "Carlos é médico OU Ana não é perita criminal. A negação de "Ana é perita criminal" não faz diferença nenhuma para ao valor lógico nesse caso. Basta que tenhamos o "Carlos é médico" = V na DISJUNÇÃO para que o valor da preposição composta seja verdadeira, independendo do valor lógico de "Ana não é perita criminal"
Assim,
a) Carlos não é médico
ERRADO, já que se descobriu na premissa III que Carlos é médico, sim
b) Carlos é médico e Ana é perita criminal
ERRADO. É impossível saber se Ana é perita criminal. Não podemos garantir isso.
c) Carlos é médico se, e somente se, Ana é perita criminal
ERRADO. Não existe nenhuma relação entre as duas coisas
d) Carlos é médico ou Ana não é perita criminal.
CORRETA. Basta que Carlos seja médico para que a disjunção seja verdadeira.
e) Ana é perita criminal
ERRADO. Não sabemos o valor dessa preposição.
Espero ter contribuído!
-
MÉTODO DAS PREMISSAS VERDADEIRAS: Encontrar uma premissa simples ou uma conjunção (E), julgar todas as premissas verdadeiras, caso a conclusão seja verdadeira, o argumento será válido. Caso a conclusão seja falsa, o argumento será inválido.
A (V) => B (V)
C (?) => D (V)
D (V) e A (V)
--------------------
B (V) ou C (V-F)
Assim, a única alternativa que dará certeza de que o argumento será válido será a D: (Carlos é médico) OU (Ana não é perita criminal). A negação de (Ana é perita criminal) não faz diferença nenhuma para ao valor lógico nesse caso. Basta que tenhamos (Carlos é médico) = V na DISJUNÇÃO para que o valor da preposição composta seja verdadeira, independentemente do valor lógico de (Ana não é perita criminal).
-
Já fiz diferente... Vamos lá:
considerei todas as premissas verdadeiras, lembrando que quando TODAS as premissas são VERDADEIRAS, a conclusão CONSEQUENTEMENTE será também VERDADEIRA
Premissa 1 = V
Premissa 2 = V
Premissa 3 =V
Conclusão = V
p = Carlos é legista
q - Carlos é médico
r = Ana é perita Criminal
s = Ana é policial civil
Transcrevi as premissas 1,2,3 e ficou :
(I) p -> q = V
(II) r -> s = V
(III) s ^ p = V ( como é uma conjunção eu desmembrei, logo ( s= V ) e (p= V)
Tendo o valor de S e de P , substitui na premissa (I):
(I) p -> q = V
(I) V -> q = V
logo q= V
Tendo o valor de S e de P , substitui na premissa (II):(II) r -> s = V
(II) r -> V= V
Logo r = V/F
P = VQ= VR = V/FS = V
Agora analisaremos cada alternativa . Lembrando que é um ARGUMENTO VÁLIDO, logo se todas as premissas foram consideradas verdadeiras, OBRIGATORIAMENTE a conclusão será VERDADEIRA.
a) Carlos não é médico = F , Como a resposta deu F, ERRADA
b) Carlos é médico e Ana é perita criminal = 1) V ^ F = F 2) V ^ V = V Como a resposta deu tanto V quanto F, ERRADA.
c) Carlos é médico, se somente se, Ana é perita Criminal 1)V v (exclusivo) V = F 2) V v (exclusivo) F = V Como a resposta deu tanto V quanto F , ERRADA.
d) Carlos é médico ou Ana não é perita criminal 1) V v V= V 2) V v F = V , em ambas as condições a conclusão dara V. CORRETA.
e) Ana é perita Criminal , pode ser tanto V quanto F. ERRADA
.
-
Se for fazer por essas grandiosas tabelas acabará o tempo de prova.
Basta fazer premissas verdadeiras; conclusão verdadeira = Argumento Válido.
-
Devo estar cometendo algum equívoco, mas discordo do gabarito. A letra D é montada da seguinte forma:
B v C (Gabarito).
No entanto, entendo que o correto deveria ser:
B v ~C ( Ana não é perita criminal).
Semelhantemente, a letra e) deveria ser:
C (Ana é perita criminal).
Onde estou errando ?
Grato,
Jorge.
-
Concordo com Fabiano P. , esse tipo de solução com tabela verdade não cabe para prova de concurso. Perde-se muito tempo.Diversos colegas apresentaram tipo de solução mais efeiciente.
-
A d) está correta simplesmente por dizer que Carlos é médico, pois para a alternativa estar certa basta que uma das duas colocações (...ou...) esteja correta.
A própria questão coloca "um argumento válido é...", e não "conclui-se logicamente..."
Não é logicamente impossível que Carlos seja médico E Ana não seja perita, por exemplo. Só não é uma conclusão lógica, é uma possibilidade.
-
Se admitirmos que Ana é perita, teremos duas respostas corretas. Então só pode ser a letra D.
-
Obs1: Considerar que todas as premissas são verdadeiras;
Obs2: Iniciar sempre pelas premissas simples ou pela pela conjunção "e"
V V
Se Carlos é legista, então ele é médico. - (Se então, não pode dar V e F)
F V
Se Ana é perita criminal, então ela é policial civil. - (Se então, não pode dar V e F)
V V
Ana é policial civil e Carlos é legista. - (iniciar pela conjunção "e"), será verdade quando as duas premissas são verdadeiras.
Conclusão:
Ana é policial civil;
Ana não é perita;
Carlos é Legista;
Carlos é médico.
-
Isaac Carvalho, nao se pode afirmar que ana é perita, pois no "se,...entao" pode dar V e V tambem
-
Para que a premissa III seja verdadeira, o valor de ambas as preposições (Ana é policial civil E Carlos é legista) deverá ser verdadeiro (V ^V= V)
A partir daí, se descobre na premissa II que a preposição "Carlos é médico" é verdadeira, porque não poderá ser falsa para que a condicional seja verdadeira.
Na premissa II, fica impossível se afirmar o valor de "Ana é perita criminal", pois essa preposição pode ser tanto F quanto V para que a condicional seja verdadeira.
Assim, a única alternativa que dará certeza de que o argumento será válido será a D, "Carlos é médico OU Ana não é perita criminal. A negação de "Ana é perita criminal" não faz diferença nenhuma para ao valor lógico nesse caso. Basta que tenhamos o "Carlos é médico" = V na DISJUNÇÃO para que o valor da preposição composta seja verdadeira, independendo do valor lógico de "Ana não é perita criminal"
Assim,
a) Carlos não é médico
ERRADO, já que se descobriu na premissa III que Carlos é médico, sim
b) Carlos é médico e Ana é perita criminal
ERRADO. É impossível saber se Ana é perita criminal. Não podemos garantir isso.
c) Carlos é médico se, e somente se, Ana é perita criminal
ERRADO. Não existe nenhuma relação entre as duas coisas
d) Carlos é médico ou Ana não é perita criminal.
CORRETA. Basta que Carlos seja médico para que a disjunção seja verdadeira.
e) Ana é perita criminal
ERRADO. Não sabemos o valor dessa preposição.
Créditos: Silas123 "Aprova Concursos"
-
É complicado explicar esse tipo de questão,mas para os que já sabe a questão deu conectivo (e) coloca v nas duas premissas e pra cima da banca
-
tá maluco...
-
Como o enunciado não mente:
(Ana é polícia civil E Carlos é legista = V)
Na conjunção E só é V quando ambos forem verdadeiros
Se Carlos é legista (V), então ele é médico (V)
Se Ana é perita (não sei), então ela é policial civil (V)
Ana é policial civil (V) e Carlos é legista (V) ------------ conectivo E ambos são "V"
Corrijam-me se estiver errado por favor!
Vlwwwwwwww
-
I. CL (V) -> CM (V) = V
II. AP (V/F) -> A.PC (V) = V
III. A.PC (V) ^ CL (V) = V
Alternativa D
-
Olha só....para montar-mos este tipo de questão é preciso
conhecer a tabela verdade e suas regras. até ai sem novidades.
I. Se Carlos é legista, então ele é médico.
II. Se Ana é perita criminal, então ela é policial civil.
III. Ana é policial civil e Carlos é legista.
somente na opção três podemos ter certeza de que ANA É PC E CARLOS É LEGISTA, pois temos o conectivo de conjunção, onde as duas tem que ser VERDADEIRAS.
sendo assim, posso atribuir os valores das demais premissa.
I. Se Carlos é legista, então ele é médico. ( 1ªV. A SEGUNDA PRECISA SER V TMB)
V ------> V
II. Se Ana é perita criminal, então ela é policial civil. (2ª V. A PRIMEIRA PODE SER TANTO FALSA QUANDO VERDADEIRA)
V / F ----------> V
III. Ana é policial civil e Carlos é legista.
V ^ V
conclução: Ana é PC
Ana pode ou não ser Perita Criminal
Carlos é legista
Carlos é médico
-
Vamos lá,
Primeiro passo é deixar a premissa III verdadeira;
A policial ^ C legista = V ^ V
A partir daí, suba e deixe as outras premissas verdadeiras;
C legista ---> C médico = V ---> V
A perita ---> A policial = ? ---> V
Agora iremos as conclusões;
A) Carlos não é médico F
B) Não podemos afirmar se Ana é ou não perita, portanto, poderia ser V ou F, sendo F a conjunção seria Falsa
C) Mesmo caso acima, por não podermos afirmar se Ana é ou não perita, então a bicondicional poderia ser V ou F
D) Apenas o fato de sabermos que Carlos é médico é o suficiente pra concluirmos que a proposição é V, pois o valor da proposição, Ana não é perita, poderia ser V ou F que não faria diferença.
E) Não podemos afirmar.
-
Gabarito D.
Usa do o método da Conclusão Falsa fica melhor.
Considere as conclusões falsas e teste uma a uma nas premissas.
Como saber se o argumento é válido? Simples, quando afirmado que todas as premissas são verdadeiras e pelo teste você conseguir achar uma premissa falsa,significa que a conclusão falsa adotada não poderia acontecer,logo argumento válido!
Resumindo: Adota conclusão FALSA.
PREMISSAS VERDAEIRAS> ARGUMENTO INVÁLIDO
PREMISSAS FALSAS,BASTA UMA!> ARGUMENTO VÁLIDO.
FORÇA!
-
Alguma alma caridosa explica por que a B está errada?
Se considerar a preposições verdadeiras as premissas também o sarão! Onde estou errando?
V V
I Se Carlos é legista, então ele é médico. = V
V V
II. Se Ana é perita criminal, então ela é policial civil. = V
V V
III. Ana é policial civil e Carlos é legista. = V
V V
Carlos é médico e Ana é perita criminal. = V
-
Também fiquei muito confuso nesta questão, mesmo com a explicação do professor e dos colegas, porem, o que vejo como a letra D como a resposta correta é que após a tabela verdade entreb as colunas A) B) c)b d) e)....a quem tem mais proposições dita como verdadeira é justamente a alternativa "D", totalizando 12 verdadeiras.....será que tem alguma coisa a ve?
-
I. Se Carlos é legista(3°V), então ele é médico(4°V).
II. Se Ana é perita criminal(6° V ou F INDETERMINAÇÃO ? ), então ela é policial civil(5°V).
III. Ana é policial civil(1°V) e Carlos é legista(2°V).
Carlos é médico ou Ana não é perita criminal.
TABELA DO CONECTIVO OU BASTA QUE UMA SEJA V PARA QUE O RESULTADO FINAL SEJA VERDADEIRO.
Gabarito Letra D.
Bons estudos!
-
GAB. D)
Carlos é médico ou Ana não é perita criminal.
-
Gabarito:D
Principais Regras:
- 50% das questões é para você verificar se o argumento é válido ou inválido e 50% é para você achar a conclusão. O método de RESOLUÇÃO é o mesmo.
- Às vezes, a banca coloca sinônimos, então atenção, pois 99,9% das questões que aparecerem sinônimos das palavras, você continuará resolvendo da mesma forma.
- Como identificar se o argumento é válido ou inválido? Passos: 1) Transformar as frases em siglas; 2)A conclusão vai ser SEMPRE FALSA e as premissas SEMPRE VERDADEIRAS; 3) Solucionar; 4) Se ao final, você resolver tudo sem encontrar erro, o argumento será inválido e se encontrar alguma divergência durante a resolução, será argumento válido.
Ex: A: Igor foi estudou e passou; B: Igor estudou; Conclusão: Igor passou;
1) Transformar as frases acima em siglas ou termos reduzidos - eu coloquei a primeira letra de cada termo, mas você pode fazer do jeito que for melhor, mas o intuito é reduzir as frases, logo ficará:
A (E ^ P); B (E); Conclusão (P)
2) As 2 primeiras sentenças serão as premissas que colocarei o valor final de verdadeiro e a conclusão de falsa. Logo, ficará:
A (E ^ P) = V; B (E) = V; Conclusão (P)= F
3) Solucionar
A única alternativa para solucionar é a premissa A. Logo ficará:
A (V ^ F) = V ?
No conectivo "e" quando se tem V ^ F, o final será Falso, logo ocorreu uma divergência.
4) Divergência, logo argumento válido.
- Já em relação as questões para achar a conclusão? O método descrito acima é aplicado, porém você deverá iniciar por sentenças simples, depois conectivo "e" e assim sucessivamente. Costumo dizer que é um pirâmide, a cada premissa resolvida, novas premissas serão abertas para você achar seu valor final. Geralmente existem diversas conclusões. CUIDADO: Exemplo: Premissa A: Carlos foi a festa; No momento que você identificar ao resolver que essa premissa é falsa, a conclusão trocará o valor semântico da frase, logo será "Carlos não foi a festa".
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação !!
-
Antecedente da premissa II pode ser tanto V quanto F. Então, não dá para dizer NECESSARIAMENTE qual seja. O gabarito é uma conjunção e uma delas temos certeza que é V, então não importa o valor da outra premissa que não sabemos, será necessariamente Verdadeiro.