-
Bem galera, corrijam-me caso eu esteja errado, mas entendi da seguinte forma:
Existem 6 homens para entrar em 3 barcos de maneira aleatória, a questão pergunta do barco vermelho ter saído com 5 homens do porto
A chance do 1º homem ir para o barco vermelho é 1/3;
A chance do 2º homem ir para o barco vermelho também é 1/3, e assim por diante até o 5º homem (já que são eventos independentes). Logo a chance do barco vermelho ter 5 homens é:
1/3 * 1/3 * 1/3 * 1/3 * 1/3 = 1/243 = 0,004 que é inferior a 0,04
-
Victor e Ricardo, acredito que não esteja correto o pensamento.
Se fizéssemos somente (1/3)^5, onde, no cálculo, estaria o sexto homem? Pois ele também tem a probabilidade de entrar no barco vermelho e, se tivesse, não seria o caso que a questão está se referindo.
Não sei calcular por meio de fórmula. Mas acho que deveríamos calcular todas as possibilidades de os turistas se dispersarem nos 3 barcos (calculei 60) e depois saber as possibilidades de terem exatamente 5 no vermelho (calculei 2, sendo a primeira possibilidade com 5 no vermelho e 1 no azul e a segunda possibilidade com 5 no vermelho e 1 no amarelo). Daí fazer a divisão (2/60) e saber a probabilidade. Achei aqui 0,0333 como resposta.
Lembrando que não importa qual homem exatamente está em qual barco... somente a quantidade de homens em cada barco.
-
Bom pessoal entendi assim:
Distribuindo-se aleatoriamente os homens em três barcos temos pelo PFC: 6x5x4=120
Se já temos o barco vermelho com 5 ocupantes então só restam 2 possibilidades que seriam: o barco amarelo com 1 e azul 0, e o amarelo 0 e azul 1.
Logo 2 possibilidades em um universo de 120: 2/120 = 0,01666667
Gabarito Errado
-
Coloft Aduba o calculo do Vitor está correto, o sexto homem não pode estar no barco, pois só cabem 8. Como ja tinha3 mulheres, cabia somente mais 5 homens, logo 1/3.1/3.1/3.1/3.1/3 = 1/243 = 0,004
-
As
mulheres se dividiram em 3 grupos de 3 mulheres, tendo cada grupo ocupado um
dos três barcos. Sendo assim e cada barco restaram 5 lugares para serem
preenchidos pelos 6 homens.
Assim a probabilidade de que o barco
vermelho saia com 5 homens será de
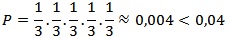
Onde 1/3 é a chance do 1° homem entrar
no barco vermelho, o 2° entrar também no barco vermelho até completar o 5°
homem. Onde 3 é o número de barcos que temos.
Resposta:
ERRADO.
-
Pensei diferente:
Vamos lá....
P = 1/3 * 1/3 (precisamos de dois homens para o barco vermelho). Agora que já conseguimos o que queríamos, precisamos achar a probabilidade dos homens restantes não irem para o barco vermelho:
P = 2/3 * 2/3 * 2/3 * 2/3.
Multiplicando as duas probabilidades = 1/9 * 8/81 = 0,010.
-
Heitor Liuth:
Veja que a pergunta é a probabilidade de deixar o porto com 5 TURISTAS HOMENS.
O seu cálculo é para o barco vermelho deixar o porto com 5 turistas no total.
-
Temos 6 homens para distribuir em 3 barcos, porém cada barco só comporta mais 5 homens, pois já tendo 3 mulheres cada, e a lotação máxima de 8, só teríamos a possibilidade de mais 5 homens por barco.
Assim, a possibilidade de distribuição dos homens é 5x5x4 = 100. (primeiro barco tenho 6 homens mas só 5 possibilidades, segundo barco tenho 5 homens e cinco possibilidades, terceiro barco tenho 4 homens e 5 possibilidades).
Contudo, havendo o preenchimento de 5 homens no barco vermelho, termos duas possibilidades: azul 0 e amarelo 1, ou azul 1 e amarelo 0, o que nos dá 2 possibilidades.
Portanto, 2/100 = 0,02. Que é < que 0,04.
-
1ª solução (aproximada)
Se desprezarmos o fato que não podem todos os 6 homens no mesmo barco:
C(6,5) x (1/3 X 1/3 X 1/3 X 1/3 x 1/3 x 2/3)= 6 x (2/729)= 12/729= 4/243 = 0,01646 < 0,04.
A probabilidade é inferior a 0,04 (ITEM ERRADO, o que coincide com o gabarito oficial divulgado pelo Cespe.
Em tempo:
1) Tem que multiplicar pela Combinação de 6, 5 a 5: são 6 homens diferentes, sendo 5 homens no barco vermelho. C(6,5) =6!/(1!.5!) = 6.
2) O último 2/3 é por que o 6º passageiro não pode ocupar o barco vermelho: ele pode ocupar o barco amarelo ou azul (2 possibilidades, entre 3 barcos possíveis para esse passageiro).
A diferença é muito pequena, por isso valeria à pena essa solução por aproximação.
2ª solução (cálculo exato)
1º) Universo Amostral: Determinar de quantas maneiras 6 homens podem se distribuir em 3 barcos:
___ ___ ___ ___ ___ ___ 3 x 3 x 3 x 3 x 3 x 3 = 729.
Desses 729 modos, 3 deles devem ser excluídos (6,0,0) (0,6,0) e(0,0,6), pois não podem ficar todos os homens no mesmo barco: 729 – 3 = 726, uma vez que a capacidade máxima do barco é de 8 ocupantes.
Em cada barco, há sempre 3 mulheres. Se todos os 6 homens ficarem no mesmo barco, teríamos 3 + 6 = 9 ocupantes, o que não é possível, de acordo com o enunciado. Logo o Universo amostral tem 726 elementos.
2º) Evento E: “o barco vermelho deixou o porto com 5 turistas homens”.
Com 5 homens no barco vermelho, resta 1 turista para o barco azul ou para o amarelo.
Total de possibilidades: ___ ___ ___ C(6,5) x 2 x 1 = 6 x 2 = 12.
[barcos vermelho e azul (5,1,0) são 6 possibilidades; barcos vermelho e amarelo (5,0,1) também 6 possibilidades. 6+6 = 12].
3º) Probabilidade do Evento E: P(E) = 12/726 = 2/121 = 0,0165 < 0,04.
A probabilidade é inferior a 0,04 (ITEM ERRADO, o que coincide com o gabarito oficial divulgado pelo Cespe.
-
Tem que decompor e fazer devagar...
O espaço amostral para encaixar um homem é 3. e como trata-se de 1 homem por vez, 1/3.
Acontece que estamos falando da alocação de 5 homens...
Então tem que repetir essa operação p/ cada homem.
-
Pessoal, depois de muito ler os comentários aqui, vou tentar simplificar...
Bom a questão envolve princípios de contagem com probabilidade. Portanto, a primeira pergunta é: utilizo a fórmula do Arranjo ou a da Combinação para descobrir o numero de eventos (formas que os homens se organização nos barcos)? Só utiliza-se a combinação (maioria dos casos) nos eventos em que a mistura, distribuição dos elementos em subconjunto não modifique a estrutura, exemplo: (banana, maçã, pera) é igual a (pera, maçã, banana), no nosso caso (9 pessoas no primeiro barco, 3 no segundo, 3 no ultimo) é diferente de (3 no primeiro, 3 no segundo, 9 no último), portanto devemos usar o Arranjo para identificar o número de eventos possíveis. A=n!/(n-p)!.
A=6!/(6-3)!, ou seja, quero distribuir 6 homens em 3 lugares diferentes de todas as formas possíveis.
A=6!/(6-3)! = 120
Sabendo agora que existe 120 maneiras de organizar 6 homens em 3 barcos, agora tenho que saber quantas possibilidades o examinador quer que eu teste. " a probabilidade de o barco vermelho ter deixado o porto com 5 turistas homens", sendo assim, só poderá ocorrer o evento desejado nas seguintes hipóteses (3,8,4) ou (4,8,3), por fim existem 2 possibilidades para 120 eventos, 2/120=0,01666
-
Vladson nesse arranjo estão incluídas as hipóteses de 6 homens em algum dos barcos? Elas não deveriam ser excluídas do total de maneiras possíveis? Ficaria 120 maneiras - 3 impossíveis (6 homens no barco amarelo ou 6 homens no barco vermelho ou 6 homens no barco azul) = 117 maneiras
-
nº H = 6
Após distribuir 1 H em um barco, restam 5H para serem distribuídos em 2 barcos (2 possibilidades em 100% ).
2 / 100 = 0,02
-
Vídeo aula sobre esta questão, por favor!!
-
Nossa, cilada esses comentários. Resposta E. Solução:
V = Vermelho;
X = Outro barco que não for o vermelho.
VVVVX = 1º escolhe V, o resto tb, exceto o último, que escolhe X.
A probabilidade que a questão pede é:
Prob de VVVVX + Prob de VVVXV + Prob de VVXVV + Prob de VXVVV + Prob de XVVVV
Então:
P = 1/3^5 + 2*5/3^6
P = 1/243 + 10/729 ~= 0,004... + 0,013....
Essa seria a resposta "correta". Provavelmente o que o Cespe queria, por conta desse "4" aí.
Mas tem outra forma de resolver essa questão, depende do seguinte:
"se os turistas homens se distribuíram nos barcos de maneira aleatória"
É aí que tá, aleatório é ser sorteado para o barco A,B ou C? Aleatório é ser sorteado para o ASSENTO X do barco Y?
Se aleatório é sentar em qualquer assento(improvável, mas enfim), então vamos lá:
São 15 assentos restantes, se o 1º homem escolher o barco vermelho, o 2º ir pro mesmo barco não é 1/3(5/15), é menos, passa a ser 4/14, pois agora tem apenas 4 vagas no vermelho e 14 vagas totais para ele escolher.
Vou ser bem didático:
Temos que somar as probabilidades VVVVVX, VVVVXV, VVVXVV, VVXVVV, VXVVVV, XVVVV (V = Vermelho; X = Outros Barcos).
Para o caso VVVVVX
1º homem escolhe o vermelho: 5/15 de prob.
2º escolhe o vermelho: 4/14 de prob.
3º escolhe o vermelho: 3/13 de prob.
4º escolhe o vermelho: 2/12 de prob.
5º escolhe o vermelho: 1/11 de prob.
6º escolhe sem ser vermelho(X): 10/10 de prob.
Prob de VVVVVX = [5! / (15*14*13*12*11)]
Para o caso XVVVVV
1º escolhe sem ser vermelho(X): 10/15 de prob.
2º escolhe o vermelho: 5/14 de prob.
3º escolhe o vermelho: 4/13 de prob.
4º escolhe o vermelho: 3/12 de prob.
5º escolhe o vermelho: 2/11 de prob.
6º escolhe o vermelho: 1/10 de prob.
Prob de XVVVVV= [5! / (15*14*13*12*11)]
Note então que todos os casos sempre dão no mesmo valor, então a probabilidade total é 6 * [5! / (15*14*13*12*11)]
Simplificando, teremos
P = 4/(14*13*11) = 4/2002 = 2/1001 ~= 0,001998
Para provar que não é viagem minha, vou resolver usando só Combinatória, vai chegar no mesmo resultado.
P = [Possibilidades de 5 no vermelho e 1 em qualquer outro] / [Todas as possibilidades]
[Possibilidades de 5 no vermelho e 1 em qualquer outro] = C5,5 * C10,1 = 10. É fácil de imaginar. Se 5 homens terão que ficar no vermelho, então um outro vai escolher uma das 10 vagas, somando 10 possibilidades totais.
[Todas as possibilidades] = C15,6 = 15!/(6! * 9!)
P = 10 / [15!/(6! * 9!)] = (10 * 6! * 9!) / 15!
P = (10*6!) / (15*14*13*12*11*10) = 6! / (15*14*13*12*11)
Novamente, P = 4/(14*13*11) = 4/2002 = 2/1001 ~= 0,001998
-
Pessoal, de acordo com o professor Vinícius Werneck a resolução é esta:
Gabarito: errado.
As mulheres se dividiram em 3 grupos de 3 mulheres tendo cada grupo ocupado um dos três barcos.
Sendo assim, em cada barco restaram cinco lugares para serem preenchidos pelos seis homens. Assim a probabilidade de que o barco vermelho saia com cinco homens será de:
P= 1/3 X 1/3 X 1/3 X 1/3 X 1/3 ( o resultado dessa multiplicação é aproximadamente) 0,004, ou seja, menor que 0,04.
Sabendo que 1/3 é a chance do 1º homem entrar no barco vermelho, o 2º entrar também no barco vermelho até completar o 5º homem e o "3" é o número de barcos que temos.
Boa sorte!
-
Fiz da seguinte forma:
1º ) a probabilidade de estar em um dos três barcos é 1/3
2º ) a probabilidade de 5 homens escolherem um mesmo barco é (1/6).(1/5).(1/4).(1/3).(1/2), pois à medida que um escolhe haverá dedução em uma unidade do denominador.
3º ) juntando os dados do 1º e 2º temos: (1/3).(1/6).(1/5).(1/4).(1/3).(1/2) menor que 0,04.
-
Fiz de forma diferente dos colegas,através de arranjo. Por favor, se o raciocínio estiver incorreto, me avisem!
Quantas formas existem para alocar os homens nos barcos? A(6,3) = 6*5*4 = 120. Porém, temos 3 opções em que vão 6 homens no mesmo barco, o que não é permitido. Logo, 120-3 = 117. O universo então é formado por 117 possibilidades.
Quantas formas existem para alocar 5 homens no barco vermelho?
Barcos: Amarelo Vermelho Azul
0 5 1
1 5 0
Logo, 2 possibilidades para alocar 5 homens no barco vermelho. Então a probabilidade seria: 2/117 = 0,02 (inferior a 0,04).
-
ERRADO
amarelo - 5 ou 4 ou 3 ou 2 ou 1 ou 0 = 6 possibilidades
vermelho - 5 ou 4 ou 3 ou 2 ou 1 ou 0 = 6 possibilidades
azul- 5 ou 4 ou 3 ou 2 ou 1 ou 0 = 6 possibilidades
6*6*6 = 216
1 = 0,0046
216
-
A probabilidade dos 5 terem escolhido entrar no vermelho é de 1/3
Supondo que os 5 primeiros estraram no barco vermelho
A quantidade de formas que as pessoas podem ser escolhidas é 6/6 o primeiro , o segundo 5/6 , 4/6,...3/6,...2/6
6/6 x5/6 x 4/6 x 3/6 x 2/6 = 60 x 2 / 6x6x6x6 = 20 / 6x6x6 = 5/9x6 = 5/54 x 1/3 = 5/162 = 0,03
-
As mulheres se dividiram em 3 grupos de 3 mulheres, tendo cada grupo ocupado um dos três barcos. Sendo assim e cada barco restaram 5 lugares para serem preenchidos pelos 6 homens.
Assim a probabilidade de que o barco vermelho saia com 5 homens será de
1/3*1/3*1/3*1/3*1/3 = 0.004
Onde 1/3 é a chance do 1° homem entrar no barco vermelho, o 2° entrar também no barco vermelho até completar o 5° homem. Onde 3 é o número de barcos que temos.
Resposta: ERRADO.
-
Cada homem pode escolher 1 dos 3 barcos. Assim, a chance de cada um deles escolher o barco vermelho é de ⅓, e a chance de cada um escolher outro barco é de ⅔. Assim, a probabilidade dos 5 primeiros escolherem o barco vermelho E o último escolher outro barco é:
P = (⅓)x(⅓)x(⅓)x(⅓)x(⅓)x(⅔) = 2 / 3^6 = 2/729
Considerando que qualquer um dos 6 homens pode ser aquele que escolhe outro barco (que não o vermelho), devemos multiplicar a probabilidade acima por 6, ficando com:
P = 6 x 2/729
P = 2 x 2 / 243
P = 4 / 243
P = 0,016
Este valor é INFERIOR a 0,04, de modo que o item está ERRADO.
-
Pessoal, esta questão pode ser resolvida por uma ferramenta muito interessante : teorema binomial!!!
-
Eu fiz usando binomial: P(k,n,p) = C(n,k)*p^k *(1-p)^n-k
k = 5 numero de sucessos (nesse caso 5 homens no mesmo barco)
n = numero de individuos que eu tenho pra distribuir (nesse caso 6 homens)
p = probabilidade de sucesso, (nesse caso 1/3, já que em cada tentativa temos 1 homem pra 3 barcos)
Aplicando a formula:
C(6,5)* (1/)^5 * (1-1/3)^6-5 = 0,0165
-
Cada homem pode escolher 1 dos 3 barcos. Assim, a chance de cada um deles escolher o barco vermelho é de
⅓, e a chance de cada um escolher outro barco é de ⅔. Assim, a probabilidade dos 5 primeiros escolherem o
barco vermelho E o último escolher outro barco é:
P = (⅓)x(⅓)x(⅓)x(⅓)x(⅓)x(⅔) = 2 / 3^6 = 2/729
Considerando que qualquer um dos 6 homens pode ser aquele que escolhe outro barco (que não o vermelho),
devemos multiplicar a probabilidade acima por 6, ficando com:
P = 6 x 2/729
P = 2 x 2 / 243
P = 4 / 243
P = 0,016
Este valor é INFERIOR a 0,04, de modo que o item está ERRADO.
FONTE: DIREÇÃO CONCURSOS
-
Entao, eu nessas questões desenho.
Bom o que temos na questão: 15 turistas 3 barcos ( 1 amarelo, 1 vermelho e 1 azul).
Bom vamos desenhar os barcos e as vagas pra nao nos perdemos
Amarelo __ __ __ __ __ __ __ __
Vermelho __ __ __ __ __ __ __ __
Azul __ __ __ __ __ __ __ __
Segundo o enunciado, existem 9 mulheres, divididas em 3 grupos
1° grupo 3 mulheres
2° grupo 3 mulheres
3° grupo 3 mulheres
Amarelo __ __ __ __ __ __ __ __
Vermelho __ __ __ __ __ __ __ __
Azul __ __ __ __ __ __ __ __
Bom, vamos dividi-las nos barcos, pouco importa onde vamos coloca-las, o enunciado só pede que tem que ter 3 mulheres em cada barco.
Amarelo M M M __ __ __ __ __
Vermelho M M M __ __ __ __ __
Azul M M M __ __ __ __ __
Agora, o enunciado pede qual a probabilidade que no barco amarelo tenham 5 homens correto? Assim, ele quer P (amarelo = 5 homens) e a P(azul ou vermelho = 1 homem) certo?
Bom vamos lá, vamos dar nomes para esses 6 homens que tal Joao, Antonio, Pedro, Samuel, Reinaldo e Carlos.
Sabemos que tem 3 barcos certo?
Qual a probabilidade de Joao escolher o barco amarelo? ora ele tem 3 barcos pra escolher, entao 1/3 concorda?
Qual a probabilidade de Antonio escolher o barco amarelo? ora ele tem 3 barcos pra escolher, entao 1/3 concorda?
Qual a probabilidade de pedro escolher o barco amarelo? ora ele tem 3 barcos pra escolher, entao 1/3 concorda?
Qual a probabilidade de samuel escolher o barco amarelo? ora ele tem 3 barcos pra escolher, entao 1/3 concorda?
Qual a probabilidade de reinaldo escolher o barco amarelo? ora ele tem 3 barcos pra escolher, entao 1/3 concorda?
Opa, já deu as 5 pessoas no barco certo? mas e o Carlos? o Carlos sobrou :( Bom, vamos colocar o Carluxo em um barco também,
bora lá qual a probabilidade do carlos ficar no azul ou a vermelho? ora 2/3 certo?
Boom vamos substituir no nosso desenho?
bora la
Amarelo M M M 1/3 1/3 1/3 1/3 1/3 * (2/3)
Vermelho M M M __ __ __ __ __
Azul M M M __ __ __ __ __
Então qual a probabilidade do Joao e do antonio e do pedro e o samuel e o reinaldo estarem no amarelo e o Carlos estar no azul ou vermelho? se tem "e" vc multiplica eles o que daria 2,7*10^(-3) , multiplicando por 6, já que são 6 homens, temos 0,016
Aplicando uma binomial.
P(k,n,p) = Cn,k * p^(k) * (1-p)^(n-k) correto?
vamos dar nomes aos bois:
k = o que eu quero ( 5 homens ) ui kkk
n = quantidade que eu tenho (6 homens)
p = probabilidade ( 1/3) <--probabildade do cara escolher o barco amarelo
P(5,6,1/3) = C6,5 * 1/3^(5) * (1-1/3)^(6-5) = 0,016 bate também