-
Progressão Aritmética(m, w+4, p+8)
podemos dizer então que:
w = m + 4
p = m + 8
Progressão geométrica (m, p+8, w+60), agora basta substituir o "p" por (m+8) e "w" por(m+4)
(m, m+8+8, m+4+60) = (m, m+16, m+64) Por definição, podemos dizer que: (m + 16)² = m(m+64), assim temos:
m² + 32m + 256 = m² + 64m
m² - m² + 32m - 64m = -256
32m = 256
m = 8
Sabendo o valor de 8, vamos montar a P.G.
m , (m + 16) e (m + 64)
8 , (8 + 16) e (8 + 64)
8 , 24 e 72
Assim para acharmos o valor de q, basta dividirmos xq / x, assim:
24 / 8 = 3
e/ou
72 / 24 = 3
-
Sendo PA = ( m , W , P ) de razao r = 4
entao : PA = ( m , m+4, m+8 ) pois: An = A(n-1) + r na PA.
portanto: W = m + 4
P = m + 8
Como a PG e' do tipo:
PG = ( m , P+8 , W+60 )
Substituindo os valores de W e de P, temos:
PG = ( m , m+8+8 , m+4+60 )
PG = ( m , m+16 , m+64 )
Lembrando que na PA o segundo termo e' dado por:
m+4 = [ m + m+8 ]/ 2 contudo aqui nao sera' necessario, e ..
na PG o segundo termo sera' extremamente importante sabe-lo, e e' nada
mais nada menos que a dita razao " q " que estamos procurando, e, e'
obtida por:
A2/A1 = A3/A2 = ...==> ( A2 )^2 = A1 * A3
olhando na PG quem sao os termos A1 , A2 e o A3, substituindo-os e e...
elevando o termo ao quadrado e depois isolando o m. Obs: Importante pois as vezes faz-se necessa'rio criar um sistema e ainda podera' ser uma equacao
de segundo grau, tendo que extrair as suas raizes atraves de Baskara, nao
sera' o caso deste problema, pois o termo "quadratico" sera' nulo.
( m+16 )^2 = ( m * m+64 )
entao: m^2 + 32m + 256 = m^2 + 64m
m^2 - m^2 +32m - 64m + 256 = 0
cancele termos, some os demais...
- 32 m + 256 = 0
m = [-256/-32]
m = 8
Daqui em diante e' so' substituir na PA e na PG o valor " m "
PA = ( 8 , 12 , 16 )
PG = ( 8, 24 , 72 )
onde a razao "q" da PG e' ou sera'...
24/8 = 72/24 = 3
.:. q = 3
-
PA (m, w, p)
Como a razão da PA é 4, podemos dizer então que:
w = m + 4
p = m + 8
Então a PA ficaria: (m, m+4, m+8)
Substituindo estes valores na P.G. temos:
m, (p + 8) e (w + 60)
m , (m + 8 + 8) e (m + 4 + 60)
m , (m + 16) e (m + 64)
Utilizando a Propriedade que diz: Numa PG com número ímpar de termos, o quadrado do termo médio é igual ao produto dos extremos.
Podemos dizer que: (m + 16)² = m(m+64), assim temos:
m² + 32m + 256 = m² + 64m
m² - m² + 32m - 64m = -256
32m = 256
m = 8
Sabendo o valor de 8, vamos montar a P.G.
m , (m + 16) e (m + 64)
8 , (8 + 16) e (8 + 64)
8 , 24 e 72
Assim para acharmos o valor de q, basta dividirmos um termo pelo seu anterior, assim:
24 / 8 = 3 ou 72 / 24 = 3
Logo, q=3.
-
Usando
a primeira informação onde m, w, p formam uma P.A. de razão 4:
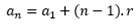
Aplicando
a fórmula acima para m, w, p:
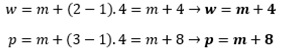
Usando
agora a segunda informação, onde os números m, (p + 8) e (w + 60) são,
respectivamente, os três termos iniciais de uma progressão geométrica de razão
q:
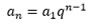
Aplicando
a fórmula acima para m, w, p:
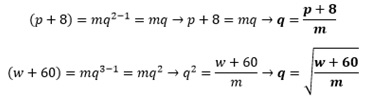
Fazendo q = q e substituindo as equações w = m + 4 e p =
m + 8:
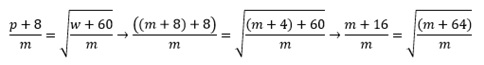
Elevando
ambos os lados ao quadrado:
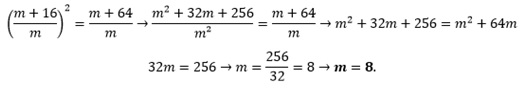
Como
p = m + 8, então p = 8 + 8 = 16
Agora
que já sabemos o valor de p e m, basta substituirmos seus valores na equação
abaixo para descobrirmos o valor da incógnita q, assim:
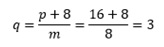
Resposta: (B)
-
Mateus, a conta deu certa, mas dizer que:
m+64 / m = 64 NÃO PODE!!!!
Em cima é uma soma, não podemos sair cortando. E numa equação, o que vc fizer de um lado da igualdade, tem que fazer no outro. Se vc manteve o lado esquerdo como estava, o raciocínio está errado. Numa próxima questão vc pode errar o resultado por causa disso.
-
Eugênia da Costa Vianna Barbosa obrigado por reparar meu erro, eu realmente não havia levado em consideração o sinal de +(adição), estaria correto se houvesse sinal de multiplicação.Ex: 64m/m = 64, peço desculpas pelo equivoco e obrigado por me corrigir afinal de contas estamos aqui para aprender ;).
-
Aprendi muito com o comentário da Alessandra
-
m,p, w E IN => m,p,w > 0
PA (m,p,w); r=4 => Equação PA an = a1 +(n-1)*r => nova PA (m,m+4, m+8); r=4
PG (m, p+8, w+60); q => Segundo a nova PA acima, p=m+4 e w= m+8 =>
nova PG (m, m+16, m+64); q
OBS: Equação PG an = a1*q^(n-1)
Sendo n=2, temos a2 = m+16 => m+16 = m* q^(2-1) => m*q - m = 16 => m*(q-1)=16 => m = 16 / (q-1)
Sendo n=3, temos a3 = m+64 => m+64 = m*q^(3 -1) => m.q2 - m =64 => m*(q2-1) = 64 => m = 64 / (q2-1)
Substintuindo o valor de m, temos;
OBS: a2-b2= (a+b)*(a-b), sendo a, b diferente 0.
64 / (q2-1) =16 / (q-1), sendo q diferente 0, temos q2-1 = (q+1)*(q-1)
64 / [(q+1)*(q-1)] = 16 / (q-1) => 64 / 16 = [(q+1)*(q-1))] / (q-1) => 4 = q+1 =>>>> q=3 (Letra B )
-
Alessandra mandou bem! Vlw!!
-
Cesgranrio bota pra lascar em todas ...
-
UAI, professor do Q esqueceu da propriedade do termo médio da PG
-
alessandra, pq deu 32 m ? não seria somente os 256, pois é o quadrado do termo medio. Então seria somente elevar ao quadrado o 16.
-
pq deu 32 m ? não seria somente os 256, pois é o quadrado do termo medio. Então seria somente elevar ao quadrado o 16.
-
Para quem tem dúvida no comentário da Alessandra, lembrem dos produtos notáveis. ( m+16 )^2 é um produto notável onde tem que fazer assim:
M ^2 + 2 x 16 x M + 16 ^2 = M^2 + 32 M + 256
No mais, leiam o comentário dela e não o do professor. Ela explicou bem melhor.
Espero ter ajudado tb. Bons estudos.
-
Complementando:
Para quem não lembra das regras de produtos notáveis: (a+b)^2 = a^2 + 2ab + b^2
Basta fazer a operação (a+b).(a+b) que dá no mesmo
Logo,
(m + 16)^2 = m^2 + 2*16m + 16^2
m^2 + 32m + 256
Só não façam (a+b)^2 = (a^2 + b^2) porque está errado!
-
muuuuuito maneiraaa
-
Eu fui por dedução
Coloquei na P.A m= 8 , W= 12, P= 16
Dai calculei a P.G M=8 , P+8= 24 , W+60= 72
Peguei 24/8= 3 ou 72/24= 3
-
Oi pessoal! Tudo bem com vocês!?
Quem puder dar uma força se inscrevendo no meu canal, ativando o sininho e indicando para os amigos, o link está abaixo. No mesmo, consta a resolução dessa questão da CESGRANRIO 2014.
https://youtu.be/SYibDZXF_8g
-
Questão resolvida no vídeo do link abaixo
https://www.youtube.com/watch?v=ugUNCWP0BtA
Bons estudos.