-
Nesta questão poderemos ter:
B = Biólogo
P = Pesquisador não biólogo
Formando os grupos de 3 pesquisadores temos:
BBP ou BPB ou PBB
Fazendo BBP temos: 14/30 x 13/29 x 16/28 = 2912 / 24360
Fazendo BPB temos: 14/30 x 16/29 x 13/28 = 2912 / 24360
Fazendo PBB temos: 16/30 x 14/29 x 13/28 = 2912 / 24360
Somando: 2912/24360 + 2912/24360 + 2912/24360 = 8736 / 24360
Reduzindo a fração:
8736 , 24360 | 2
4368 , 12180 | 2
2184 , 6090 | 2
1092 , 3045 | 3
364 , 1015 | 7
52 , 145
Resposta: 52 / 145
-
Terá que
ser escolhido 3 pesquisadores dentre os 30 existentes. Queremos saber a probabilidade
de termos 2 biólogos entre estes 3 escolhidos, assim, temos três possibilidades
de arranjos:
BBO
ou BOB ou OBB
Onde B = biólogo e O = outros.
No caso da possibilidade BBO temos :
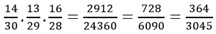
Para a possibilidade BOB temos :
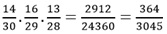
E finalmente para OBB temos :
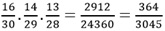
Como estamos trabalhando com "OU",sabemos que na probabilidade quando isso acontece basta somarmos os resultados das possibilidades,assim:
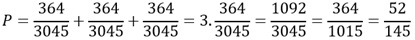
A alternativa correta é : D.
-
Alguém sabe um modo mais simples?
-
30 Pesquisadores; 14 Biólogos; 16 Não Biólogos
Possibilidades de exatamente 2 serem escolhidos:
BBN ou BNB ou NBB
BBN = 14/30 * 13/29 * 16/28 = 2912 / 24360
BNB = 14/30 * 16/29 * 13/28 = 2912 / 24360
NBB = 16/30 * 14/29 * 13/28 = 2912 / 24360 (MMC 24360)
P = 8736 / 24360
P = 52 / 145
-
14 biólogos e 16 não biólogos obs.: P(3,2): permutação de 3 com 2 elementos repetidos.
P(3,2)= 3!/2! = (3. 2!)/2! = 3
B B NB
14/30 . 13/29 . 16/28 . P(3,2)
52/435 . 3 = 156/435
RESPOSTA= 52/145
-
Ainda estou com dificuldade para entender.
Alguém poderia fazer passo a passo.
Obrigada!
-
Temos: 30 pesquisadores, sendo 14 biólogos, ou seja, 16 não são biólogos
Para os cálculos o ideal é usar combinação, pois a ordem não importa.
Para calcular o espaço amostral = CASOS POSSÍVEIS
C30,3 = 30x29x28x27!/27!3x2 = 4060
Calculo para escolher o evento: 2 biólogos: = CASOS FAVORÁVEIS
C14,2 = 14x13x12!/12!2 = 91
Calculo para escolher o evento: 1 não biólogo: = CASOS FAVORÁVEIS
C16,1 = 16x15!/15!1 = 16
Multiplica os resultados para obter o evento total dos casos favoráveis:
91x16 = 1456
Agora, é só calcular a probabilidade: casos favoráveis dividido pelos casos possíveis
P= 1456/4060 => simplificando fica 52/145
-
Resolução da questão https://www.youtube.com/watch?v=_YvIzfNwl9s
-
Depois de quebrar muito a cabeça, consegui entender a real razão. O que ocorre é o seguinte: como a questão pede que devem ser exatamente 2 biólogos, não pode ser menos de 2 nem mais de 2 (este "mais" que causa toda a confusão). Ou seja, se o cara sortear 3 biólogos, estará errado, por isso é necessário explorar todas as possibilidades de cada ordem, para limitar todas as probabilidades de sortear exatamente 2 biólogos, sendo assim, a ordem importa, nesse caso. Se a questão pedisse pelo menos 2 biólogos, aí então a ordem não importaria e não teria que somar as 3 frações.
-
Gabarito: D
Para resolvermos a questão, precisamos entender que são EXATAMENTE dois biólogos e um não biólogo escolhidos. Isso nos leva a entender que, achada a probabilidade, devemos multiplicar por uma permutação de 3 elementos, sendo que um elemento se repete duas vezes (biólogos). Por que? porque o enunciado só disse quem deve ser escolhido, não falou em ORDEM, portanto tanto faz ser Biólogo - Biólogo - Não Biólogo ou Não Biólogo - Biólogo - Biólogo ou Biólogo - Não Biólogo - Biólogo.
Calculando a probabilidade do primeiro caso: 14/30 (biólogo) x 13/29 (biólogo) x 16/28 (não biólogo) * P3,2 = 14/30 x 13/29 x 16/28 x 3
simplificando: 1/15 x 13/29 x 8/2 x 3 = 1/15 x 13/29 x 4 x 3 = 52/435 x 3 = 52/145.
-
Acho que vocês estão esquecendo o fato da questão EXPRESSAMENTE dizer: EXATAMENTE 2 biólogos.
Se atentarmos para esse detalhe, ela fica mais fácil.
-
P(dois biologos e um não) = Favoraveis = C14,2 * C16,1 = 91 * 16 = 52
Possíveis C30,3 4060 145
gab D