-
Usei o Diagrama de Venn para descobrir os resultados possíveis e favoráveis.
-
8 marcas de cerveja, nesse caso incluindo também o "nenhuma" já que na questão está na classificação exposta.
4 possibilidades de apenas uma escolha, sendo 3 cervejas e nenhuma a escolha de quem não bebe.
4/8 = 1/2
Gabarito Letra A)
-
Pensei que era necessário saber quantos consumidores consomem apenas um tipo de cerveja do total de frequentadores do bar pra saber a probabilidade a partir daí. Fiz através de conjuntos e ficou confuso demais. Caso alguma alma caridosa possa ajudar agradeço.
-
Tentei fazer por União de Dois Eventos e não cheguei ao resultado. Conforme o colega Wagner, só acertei pelo diagrama de Venn. Se alguém souber por alguma das quatro formas da probabilidade...
-
Eu fiz o diagrama e deu um valor totalmente diferente.. :/
-
Pessoal, façam por diagramas que é mais fácil. Ao montar, vcs verão que aqueles que consomem apenas A=30, apenas B=22 e apenas C=20, total de 72. O total de pessoas que foram entrevistadas é 144. A probabilidade de escolher 1 e que esse 1 só consuma um tipo de cerveja é: P=72/144, ou seja, 1/2!!
Gab A
-
Obrigada, Renan Martins!
Ajudou muito!
-
Resposta A, sendo que o resultado final dessa questão não será exato (muitos concursos testam nossa capacidade de aproximação de resultados).
Pelo diagrama de Venn, nós chegamos no seguinte número de consumidores:
A (total) = 48
B (total) = 41
C (total) = 40
A (somente) = 20
B (somente) = 12
C (somente) = 10
AB = 11
AC = 12
BC = 13
ABC = 5
Total de consumidores de cerveja = 20+12+10+11+12+13+5 = 83
Total de consumidores (das marcas cerveja e nenhuma) = 83 + 46 = 129
Pulo do gato: pode-se considerar os consumidores de nenhuma marca como NÃO consumidores de cerveja. Portanto, ficarão de fora do espaço amostral final. Então:
Evento: A (somente) + B (somente) + C (somente) = 20+12+10 = 42
Espaço amostral: Total de consumidores de cerveja = 83
P(consumidor de cerveja de uma única marca) = 42/83 = resultado não exato, aproximadamente 1/2.
-
Primeiramente,
temos que usar o diagrama de Venn para facilitar a resolução da questão, assim:
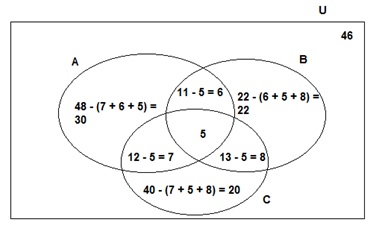
Logo,
a probabilidade pedida será:
Total
de entrevistados (Total de amostras) = 30 + 20 + 7 + 8 + 22 + 5 + 6 + 46 = 144
Total
de casos particulares que queremos = 30 + 20 + 22 = 72
Probabilidade
P = 72/144 = 18/36 = ½
RESPOSTA: (A)
-
Eu acertei, mas uma coisa me chamou atenção: como é que considero uma pessoa consumidora sem que ela consuma? Então, o comando da questão deveria ser: escolhendo um frequentador ao acaso ...
-
USEM O DIAGRAMA !!!!
-
Quase endoidei com esse calculo de EDER CHERRUTI, teu calculo ta errado irmao.
O correto e:
apenas A = 30
apenas B= 22
apenas c= 20
72 / 144 = 1/2
-
Simon Mendes, como resolveu?
-
Tem que fazer primeiro o diagrama pra descobrir o total de pessoas e os que apenas consomem A,B e C.
Fazendo o diagrama ,encontra:
A= 30 pessoas
B= 22 pessoas
C= 20 pessoas
Somando todos os valores do diagrama ,incluindo as intersecções (30+6+5+22+7+8+20)=98 Soma 98 com os 46 que não consomem ,resulta em 144.
Como o que interessa são os que apenas consomem (A,B e C),soma os três que resulta em 72.
P=72/144 ,simplificando ...O resultado será 1/2 LETRA A
-
Como vocês chegaram aos valores dos consumidores de apenas A, apenas B e apenas C?
Quando eu faço dá A=20, B=12 e C=10.
-
Nossa, finalmente entendi pq meus valores de A, B e C estavam errados: eu estava chegando em A=20, B=12 e C=10, aí percebi olhando os comentários que o eu estava considerando:
"A e B" = 11
"A e C" = 12
"B e C" = 13
E esqueci de subtrair desses valores o número 5 referente a "A, B e C".
Ou seja, o correto é:
"A, B e C" = 5
"A e B" = 6
"A e C" = 7
"B e C" = 8
A (somente) = 30
B (somente) = 22
C (somente) = 20
-
Pra quem tem facilidade com diagrama de Venn ficou muito fácil de analisar e chegar aos números, pois o enunciado deu todos os dados.
Questão top!
-
Vou comentar porque tem um monte de gente viajando nas respostas aí. Muita gente explicou como é o jeito correto de se fazer mas muita gente explicou de forma errada (a maioria) o mais bem explicado sem sombras de dúvidas foi o comentário da Marina Martins. Muito bom!
-
ABC = 5
A-B = 11 - ABC = 6
A-C = 12 - ABC = 7
B-C = 13 - ABC = 8
A = 48 - ABC - AB - AC = 30
B = 41 - ABC - AB - BC = 22
C = 40 - ABC - AC - CB = 22
TOTAL.: 72
Agora somamos tudo:
Nenhum = 46
30+22+20+5+6+7+8+46 = 144
72/144 simplifica e fica.: 1/2
-
Qual a probabilidade de eu aprender probabilidade?
0 dividido por 0 = sem chance