Gabarito: CERTO
Note, antes de tudo, que o examinador nos mostrou demandas inversas (com o P isolado). Para facilitar, vamos trabalhar com o Q isolado:
Ps = (3/200).Q + 1600
3Q + 320000 = 200Ps
Qs = -320000/3 + (200/3)P (função oferta)
Pd = –[1/40] Q + 4.000
40Pd = -Q + 160000
Qd = 160000 – 40P (função demanda)
A questão só quer que calculemos o novo preço após o imposto (t=800). Assim, vamos alterar a curva de oferta:
Nova oferta:
Qs = -320000/3 + 200(P – 800)
Novo equilíbrio
Qd=Qs
160000 – 40P = -320000/3 + (200/3)(P – 800)
320P = 960000
P = 3000
Note que as funções de oferta e demanda já estão dadas pelo preço.
Assim, basta que adicionemos o valor do imposto numa das funções para acharmos a quantidade de equilíbrio:
Nós sabemos que o preço pago pelo consumidor (Pd) é a soma do preço recebido pelo produtor (Ps) mais o valor do imposto “t”.
Então, temos que:
Ps + t = Pd
Vamos substituir os valores:
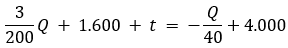
Substituindo o valor do imposto “t”:

Isolando Q:

Simplificando:

Vemos que com o imposto, a quantidade que equilibra o mercado é de 40.000 unidades.
Assim, basta substituirmos esta quantidade na função de demanda para acharmos o preço pago pelo consumidor:

Vemos que o preço pago pelos consumidores é de $ 3.000 de fato.
Se substituirmos a quantidade de 40.000 na função de oferta, teremos um preço de oferta que é exatamente a diferença entre o preço pago pelo consumidor e o valor do imposto.
Resposta: C