-
J¹+J²=C¹.i.t+C².i.t
128=C¹.1/100.2+(C¹+1600).1,5/100.2
128=C¹.2/100+(C¹+1600).3/100
128=C¹.2/100+C¹.3/100+4800/100
128=C¹5/100+48
80=5C¹/100
5C¹=8000
C¹=1600
R:C¹+C¹+1600
R:4800
-
Senhores, alguém poderia me ajudar? Onde no enunciado desta questão está dizendo que C2 = C1 + 1.600?
-
Nessa parte da questão: No segundo, de valor R$ 1.600,00 maior que o do primeiro, ou seja C2=C1+1600
-
No segundo, de valor R$ 1.600,00 maior que o do primeiro 3%=48
128 que foi o total de juros que ele pagou -48 = 80
como ele pagou n 1° empréstimo 2% e no 2° 3% divide 80 por 5=16
como no 1 emprestimo ele pagou 2 % o valor do juros pago pago foi de 32 /2=16*100=R$1600
no 2 ele pagou 3% 80-32=48+48=96/3=32*100=r$3200+1600=R$4800
-
Letra A
I) 1º empréstimo
Valor X
juros 1,0 % ao mês
prazo 2 meses
2º empréstimo
Valor (X + 1.600)
juros 1,5 % ao mês
prazo 2 meses
II) J = C*i*t
1º E: J = C*0,01*2
J = 0,02 x
2º E: J = (X + 1.600)*0,015*2
J = (X + 1.600)*0,03
J = 0,03 + 48
III) 0,02X + 0,03 + 48 = 128
0,05X = 128 - 48
0,05X = 80
X = 80/0,05
IV) X + 1.600
1.600 + 1.600 = 3.200
V) 1º E + 2º E = 1600 + 3.200 = 4.800
-
De acordo com o enunciado, tem-se:
a) empréstimo 1:
J1 = C1 x i x t
J1 = C1 x 0,01 x 2
J1 = 0,02 C1
b) empréstimo 2:
J2 = C2 x i x t
J2 = (C1 + 1600) x 0,015 x 2
J2 = 0,03 (C1 + 1600)
J2 = 0,03 C1 + 48
Como J1 + J2 = 128, tem-se:
0,02 C1 + 0,03 C1 + 48 = 128
0,05 C1 = 80
C1 = 1600
C2 = 1600 + 1600 = 3200
Finalizando, C1 + C2 = 1600 + 3200 = 4800 reais
Resposta A)
-
Empréstimo (1) = X (pago a juros de 1% ao mês, por 2 meses, totalizando 2%).
Empréstimo (2) = X + 1.600 (pago a juros de 1,5% ao mês, por 2 meses, totalizando 3%).
Juros pagos = R$ 128,00.
Resolvendo.
(2.X/100) + (3/100 * (X + 1.600) = 128/1 => (2.X/100) + [(3.X + 4.800)/100] = 128/1 => (TIRANDO O MMC) => 2.X + 3.X + 4.800 = 12.800 => 5.X = 12.800 - 4.800 => 5.X = 8.000 => X = 8.000/5 => {X = 1.600.}
E(1) + E(2) = ? => 1.600 + (1.600 + 1.600) = 4.800.
-
Juliane flenik, no enunciado diz: no 1º empréstimo de um certo valor( c1 = x), o 2º empréstimo de valor R$ 1.600,00 maior que o do primeiro, é a mesma coisa dizer que o 2º empréstimo foi de R$ 1600,00 a MAIS, ou seja, c2= x+1600; é a INTERPRETAÇÃO DA MATEMÁTICA.
-
No segundo, de valor R$ 1.600,00 maior que o do primeiro, ai
-
Simplificando:
Vamos chamar os empréstimos de A e B
O empréstimo A é representado por X + 2% (dois meses a taxa de 1%)
O empréstimo B é representado por X + 1600 + 3% (dois meses a taxa de 1,5%)
A questão diz que a soma dos JUROS da 128, então, devemos representar os empréstimo A e B em uma equação só, a fim de achar o valor de X, que é o empréstimo A. Ou seja, vamos somar as duas equações acima, representando a porcentagem por multiplicações em decimal:
0,02X + 0,03 * (X + 1600) = 128
0,02X + 0,03X + 48 = 128
0,05X = 80
X = 1600
Pronto! O primeiro empréstimo, que vale X, é de 1600. O segundo empréstimo, que vale X + 1600, vai ser 1600 + 1600, que da 3200
Somando os dois, 4800
Resposta A
-
Olá Galera boa tarde!
Vamos resolver esse exercício. Para isso vou deixar a formula de juros Simples : "J= C.i.t" no qual:
J= Juros
C= Capital
i= taxa de juros
t= tempo
Então vamos lá
O enunciado não diz qual foi o valor do primeiro empréstimo, então iremos chamar de "C1" e a taxa de juros foi de 1% ao mês e o tempo foi de 2 meses.
Como queremos achar o capital iremos fazer assim:
J1 = (C.i.T) + J2 (C1 + 1600.i.T) = 128 onde C1 é o capital do J1,
Resolvendo
______________________________________________________________________________________________________
Para ficar mais fácil e não complicar na hora de resolver irei substituir o C1 por X
J1= (x.0,01.2) + J2 ( x+1600 . 0,015.2) = 128
0,02x+(x+1600).0,03= 128
0,02x+0,03x+48= 128
0,05x+48=128 passa o 48 para depois do igual como negativo - 48 fica assim
0,05x=128-48
0,05x=80 passa o 0,05 dividindo fica: 80/0,05 que é igual a "1600"
Como no enunciado diz que " O SEGUNDO É 1600 MAIOR QUE O PRIMEIRO" temos então 1600 do capital 1 mais o 1600 como diz no enunciado, desta forma iremos achar o capital dois. Teremos então 3.200.
Veja que no enunciado ele pede " A SOMO DESSES DOIS EMPRÉSTIMO" é igual à:
Então é só somar os dois empréstimos que são: 1600 do primeiro empréstimo + o segundo que é 3.200 igual a 4.800.
ESPERO TER AJUDADO
ATÉ MAIS ;)
-
esse vídeo com a resolução da questão me ajudou bastante:
https://www.youtube.com/watch?v=Su9AnJE8NZY
-
De acordo com o enunciado, tem-se:
a) empréstimo 1:
J1 = C1 x i x t
J1 = C1 x 0,01 x 2
J1 = 0,02 C1
b) empréstimo 2:
J2 = C2 x i x t
J2 = (C1 + 1600) x 0,015 x 2
J2 = 0,03 (C1 + 1600)
J2 = 0,03 C1 + 48
Como J1 + J2 = 128, tem-se:
0,02 C1 + 0,03 C1 + 48 = 128
0,05 C1 = 80
C1 = 1600
C2 = 1600 + 1600 = 3200
Finalizando, C1 + C2 = 1600 + 3200 = 4800 reais
Resposta A)
Resposta do professor QConcursos
-
GOSTARIA DE PEDIR A AJUDA DOS COLEGAS POIS NAO ESTOU CONSEGUINDO REOLVER AS QUESTOES DE MANEIRA PRATICA SE ALGUEM PODER ME AJUDAR AGRADEÇO DESDE JA.
-
Gostei mas nao entendi pois estas questoes que envolve substituiçao sao muito dificeis para mim.
-
Gabarito: A
-
galera, sou um cara q não gosta d decorar fórmulas, portanto veja essa resolução .... basta q saiba o mínimo, ou seja, calcular juros simples sobre qualquer valor ............. na prática, se teu chefe te der um aumento d 10%, certeza q vc saberá qto vai subir no seu salário.......
dizendo q é juros simples, pode-se dizer q será O MESMO valor todos os meses.
explicando a questão:
para calcularmos APENAS o juros do primeiro empréstimo: Valor * Juros .................................... (é o q acontece pra saber EM qto subiu seu salário)
(a questão diz q são em 2 meses) = valor * juros p/ o primeiro mês + valor * juros p/ o segundo mês
(o juros é igual pra cada mês pq o juros é Simples)
para o emprèstimo 2 é a mesma coisa, só muda o valor.
(valor + 1.600) * juros p/ o primeiro mês + (valor + 1.600) * juros p/ o segundo mês
o enunciado diz q a soma dos juros é = 128
sendo juros simples, em cada mês para cada valor o juros é o mesmo. ...............
(valor * juros) + (valor * juros) + ((valor + 1.600) * juros) + ((valor + 1.600) * juros) = 128
(valor * 1%) * 2 + ((valor + 1600) * 1,5%) * 2 = 128 ......................... fazendo esse cálculo, chega-se a V = 1600
se V = 1600 e
V2= 1600 + 1600 = 3200
o enunciado pede a soma dos valores (4800)
................................ fui claro? alguém entendeu? ........... mande um ¨joinha¨ então!
-
https://www.youtube.com/watch?v=Su9AnJE8NZY
-
J = Capital x Taxa x número de meses
J = x . 0,01 . 2 (1)
J = (1600+x) . 0,015 . 2 (2)
(1) + (2)
128 = 48 + 0,05 x
x = 1600
Capital =x + (1600+x) = 1600 + 1600 + 1600 = 4800
-
Simplificando:
Vamos chamar os empréstimos de A e B
O empréstimo A é representado por X + 2% (dois meses a taxa de 1%)
O empréstimo B é representado por X + 1600 + 3% (dois meses a taxa de 1,5%)
A questão diz que a soma dos JUROS da 128, então, devemos representar os empréstimo A e B em uma equação só, a fim de achar o valor de X, que é o empréstimo A. Ou seja, vamos somar as duas equações acima, representando a porcentagem por multiplicações em decimal:
0,02X + 0,03 * (X + 1600) = 128
0,02X + 0,03X + 48 = 128
0,05X = 80
X = 1600
Pronto! O primeiro empréstimo, que vale X, é de 1600. O segundo empréstimo, que vale X + 1600, vai ser 1600 + 1600, que da 3200
Somando os dois, 4800
Resposta A
-
i A = 1% a.m ============= i B = 1,5 % a.m
____
JurosA + JurosB = 128 ------------------------ Capital B = Capital A + 1600
_____
{ [ (CapA * 0,010 * 2 meses) ] + [ (CapA+1600) * 0,015 * 2] } = 128
0,02 CapA + 0,03 CapA + 48 = 128
0,05 CapA = 80
CapA = 1600 ==========================> CapB= 1600 + 1600 = 3200
___
CapA + CapB = 1600 + 3200 = 4800
-
Eu usei as alternativas... Sorte a minha que a resposta estava na alternativa A e me poupou de fazer muitas contas...
eu subtrai os 1600 a mais de 4800 = 3200 e dividi por 2 = 1600
joguei o valor na fórmula de juros simples
J=1600*1*2/100= 32,00 (juros do Emprestimo 1)
J=3200*1,5*2/100=96,00 (juros do Emprestimo 2)
Somando os dois juros = 32,00+96,00= 128,00 Alternativa A
Na hora da prova, o que importa é acertar. Não me apego muito às fórmulas não... prefiro ir usando a lógica. Sei que elas na maioria das vezes encurtam o caminho, porém se eu não praticar a lógica e na hora esquecer a fórmula eu não resolvo a questão...
-
1º EMPRÉSTIMO - J= C*I*T === J= C*0,01*2
J= 0,02* C
2º EMPRÉSTIMO: J= C*I*T ==== J = (C+1600)*0,015*2
J= 0,03* (C+1600)
J= 0,03 C +48
SOMA DOS DOS EMPRÉSTIMOS: 0,02 *C + 0,03 *C +48= 128
0,05*C= 128-48
0,05*C= 80
C = 1600
QUEREMOS A SOMA DOS DOIS CAPITAIS: (C+1600) + C= (1600+1600) = 1600= R$ 4800,00
ALTERNATIVA A
-
https://www.youtube.com/watch?v=Su9AnJE8NZY
-
Nem precisei usar os 128 do juros, não sei se foi por um acaso mas cheguei da seguinte forma:
1° mês = 1%
2° mês = 1,5% e 1600 reais a mais
logo: 0,5% = 1600
no 1° mês ficaria 3200(porquê é 1, logo 2 * 0,5)
3200 + 1600 = 4800 ou 1600 * 3(porquê é 1,5, logo 3 * 0,5) = 4800
-
RESOLUÇÃO:
No regime de juros simples, sabemos que:
Juros = Capital inicial x taxa de juros x prazo
Ou seja,
J = C x j x t
No primeiro empréstimo, vamos chamar de P o valor do capital inicial (que não sabemos). O prazo foi de t = 2 meses, e a taxa de j = 1% ao mês. Portanto, tivemos um total de juros igual a:
J = P x 1% x 2
J = P x 0,01 x 2
J = 0,02 x P
O capital inicial do segundo empréstimo foi 1.600 reais maior que o do primeiro, ou seja, ele foi igual a P + 1.600 reais. A taxa foi de j = 1,5% ao mês, e o prazo foi t = 2 meses também. Assim, os juros pagos neste caso foram:
J = (P + 1.600) x 1,5% x 2
J = (P + 1.600) x 0,015 x 2
J = (P + 1.600) x 0,03
J = Px0,03 + 1.600x0,03
J = 0,03xP + 48
A soma dos juros dos dois empréstimos foi de 128 reais, conforme dito no enunciado. Assim, podemos escrever que:
128 = J + J
128 = 0,02xP + 0,03xP + 48
128 – 48 = (0,02 + 0,03)xP
80 = 0,05 x P
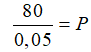
Para facilitar o cálculo, podemos multiplicar o numerador e o denominador desta fração por 100, de modo a eliminar as casas decimais. Veja:

Assim, o capital inicial do primeiro caso foi P = 1.600 reais, e o capital inicial do segundo investimento foi P + 1.600 = 1.600 + 1.600 = 3.200 reais. A soma dos valores desses dois empréstimos é igual a 1.600 + 3.200 = 4.800 reais.
Resposta: A
-
J1 + J2 = C.0,01.2 + (C + 1600) 0,015.2
128 = 0,02C + (C+1600). 0,03
128 = 0,02C + 0,03C + 48
128 = 0,05C + 48
80 = 0,05C
C = 1600
C + 1600 = 3200
3200 + 1600 = 4800
-
https://www.youtube.com/watch?v=KpNPaLQpwsg (resolução em vídeo)
Gabarito A. Bons estudos!
-
Interpretando o enunciado, sabemos que alguns desses números das alternativas diminuído 1600, e dividido por 2 será o empréstimo menor, +1600 será o empréstimo maior, aplicando cada um deles na fórmula, a soma dos juros tem que dar 128.
Me embolei pra fazer pela fórmula com os dois empréstimos de uma vez, então fui testando um de cada vez.
Logo na letra a:
4800-1600= 3200
3200/2= 1600
Ou seja, o primeiro empréstimo foi de 1600
1° J=1600.2.1/100 = 32
Já o segundo foi 1600+1600 = 3200
2° J=3200.1,5.2/100 = 96
96 + 32 = 128
Interpretar a questão é meio caminho andado.
#TJSP2021
-
fiz pelas alternativas
1600= da questão
alternativa a= 4800
4800-1600=3200
3200+1600=4800
-
Deu 128 de juros em 2 meses.
Se os juros fossem iguais em ambos os meses, renderiam exatamente 64 reais no 1º e 64 também no 2º (metade pra cada).
Porém, como o juro do 2º mês aumentou 50% em relação ao 1º mês, então, consequentemente, a distribuição dos juros (128 reais) tbm deve aumentar em 50% ("tira" 50% de juro do 1º mês e "joga" pro 2º mês). Logo, ficam 32 reais de juros no 1º e 96 reais de juros no 2º.
Agora é só aplicar na fórmula J = C i t e correr pro abraço.
-
Primeiro temos que separar as informações:
1º empréstimo: Tempo (t) = 2 meses , Taxa de juros (i) = 1% ao mês , Capital = C1 , Juros = J1
2º empréstimo: Tempo (t) = 2 meses , Taxa de juros (i) = 1,5% ao mês , Capital (C2) = C1 +1600 , Juros = J2
J1 + J2 = 128
-
Calculando o primeiro empréstimo:
J1 = C1.i.t/100
J1 = C1.1.2/100
J1 = 0,02C1
-
Segundo empréstimo:
J2 = C2.i.t/100 (substitui o J2 por 128 - J1 e o C2 por C1 + 1600)
128 - J1 = (C1 + 1600) . 1,5 . 2 / 100
128 - J1 = 3C1 + 4800 / 100
100 . (128 - J1) = 3C1 + 4800 (substitui o J1 por 0,02C1)
12800 - 2C1 = 3C1 + 4800
-5C1 = -8000
C1 = 1600
-
Por fim:
C1 + C2
1600 + 3200 = 4800
Alternativa A
-
Sopa de continhas: não consigo entender nada.
C2=C1+1600
I= 1.5
T= 2
J=X
J=[(C1+1600).1,5.2]/100
J-C1=[1600.1,5.2]/100
J-C1=48
128-48=80
C1=X
I=1
T=2
J=80
80=[C.1.2]/100=1,6
1 INVESTIMENTO
1600+1600=3,200 SOMANDO
2 INVESTIMENTO
3,200+1,600=4,800
-
resolução em vídeo:
https://youtu.be/EfRej41yAPw