-
Antes do Concurso Depois do Concurso
H=12 H=12+3x
M=8 M=8+x
Total 20 20+4x
P(H) = 0,7
P(A)=n(A)/n(U)
7/10 = (12+3x)/(20+4x)
Multiplicando cruzado:
140+28x=120+30x
2x=20
x=10
H = 12+3*10 = 12 + 30 = 42
M = 8 + 10 = 18
Total = 42 + 18 = 60
Portanto teremos após o concurso 42 homens e 18 mulheres.
Gabarito: Certo
-
Apenas corrigindo o colega Rodrigo, teremos o total de 42 homens e 18 mulheres. Total de policiais será 60.
-
Resolvi assim:
Para ter 15 mulheres entraram + 7
7 x 3 =21
21 + 12 = 33
33 + 15 = 48
Probabilidade = 33/48
= 0,68 < 0,7
Tem mais de 15 mulheres
-
De onde vocês tiraram esse 12?
-
o 12 que ele achou é o do texto , somado com os 21 , que dá 33 , pega o total de novatos com os antigos ,21 +7=28 +20 dos antigos, dará 48, aí nesse caso fica 33/48
-
Vou tentar explicar passo a passo pra quem tem dificuldades com matemática, vamos la:
1) Um batalhão é composto por 20 policiais: 12 do sexo masculino e 8 do sexo feminino... (o problema nos informa a quantidade de policiais do sexo masc. e fem.). M = 12 F = 8 ...
2) Após concurso público, sejam admitidos novos policiais no batalhão, de modo que a quantidade dos novos policiais do sexo masculino admitidos seja igual ao triplo da quantidade de novos policiais do sexo feminino...(se serão admitidos novos policiais, então vamos somar com a quantidade de existentes.
Novos policiais do sexo feminino = X ; F = 8 + X ; M = 12 + 3X (a quantidade dos novos policiais do sexo masculino admitidos seja igual ao triplo da quantidade de novos policiais do sexo feminino).
3) ...0,7 passe a ser a probabilidade de se escolher, ao acaso, um policial do sexo masculino desse batalhão...( O problema nos informa o resultado da probabilidade.
4) Sabemos que probabilidade é o evento sobre o espaço amostral, então ficará assim:P = E / S 0,7=E/SE = 12 + 3X ( ele quer a probabilidade de se escolher, ao acaso, um policial do sexo masculino, será o evento)
S = (12 +3x) + (8+x) = 20 + 4x logo, (12 +3x / 20 + 4x) = 0,7
5) Com a equação pronta, basta isolarmos o x , verificar o resultado e achar
X.0,2x = 2 -----> X = 10 no batalhão haverá mais de 15 policiais do sexo feminino.
6) voltando a fórmula do início, vamos substituir X:
F = 8 + x --> F = 8+ 10 --> F = 18, logo haverá mais de 15 policiais do sexo feminino. CORRETA...
Espero que tenham entendido,
Fé em Deus, a luta continua!!
-
Nem precisava calcular nada. Era só notar que, como a questão não disse quantos seriam os novos policiais admitidos, e que a probabilidade, após as admissões, de se escolher um homem é de 0,7, ou seja 70%, a única coisa que podemos afirmar com certeza é que no mínimo haverá 0,3 a probabilidade de ser mulher, ou seja, 30%. Então seria no mínimo 30 mulheres, o que é maior do que 15. Agora se eles tivessem colocado a quantidade de admitidos, aí a conversa seria outra, teria que obrigatoriamente fazer todos os cálculos que o DIEGGO OLIVEIRA ensinou.
-
12 + 3p / 8 + p = 7 / 3
p = 10
Foram contratados 30 homens e 10 mulheres.
Após as contratações, temos 42 homens e 18 mulheres.
Prova: 42 / 60 = 0,7.
Logo, se há 18 mulheres, há mais de 15 delas.
-
se na questão diz que tem que ser igual ao triplo de homens e mulheres é só multiplicar por 3, fica assim:
M = 3.(12) = 36
F = 3.(8) = 24
Total de 60
24 policiais femininos, questão correta!
-
Eu fiz assim:
Mais de 15, então 16 mulheres, menos 8 = 8 * 3 = 24 homens, 24 +12 = 36 homens e 16 mulheres somando 52, 70% de 52 é 36,4, ficando assim muito próximo de 70% e não exigindo fazer com o numero de 18 mulheres, pois se da certo com 18, você teria que fazer com 16 pra comprovar pois está na questão, senão eu considero como chute. Explicando, se a condição fosse maior que 14 mulheres, a conte de vocês ainda estaria certa, pois fez com 18, mas ao provar com 15 ela daria errada, tornando a questão errada.
Espero que tenham entendido.
-
Sem dúvida o melhor comentário é o do Mozart Martins, incrível, super simples.
Só para elucidar melhor o 7/3 (7 sobre 3, é referente ao valor da probabilidade que a questão nos traz)
Ficaria assim :
12 + 3x = 7
8 + x 3
Agora multiplica cruzado ( em "X" )
E ficará :
36 + 9x = 56 + 7x
Depois isola o "X"
9x-7x = 56 - 36 ---> 2x = 20 ---> x = 10
Logo :
12 + 30 = 42 ( homens )
8 + 10 = 18 ( mulheres )
Espero ter ajudado.
* Todos os créditos ao colega Mozart Martins que nos trouxe essa maneira simples e prática.
-
Antes do novo concurso, tínhamos um total de 12 policiais masculinos e 8 femininos, totalizando 20.
Depois do novo concurso o número de policiais do sexo masculino admitidos foi igual ao triplo da quantidade de novos policiais do sexo feminino, logo chamando de x o número de policiais do sexo feminino temos a tabela a baixo:
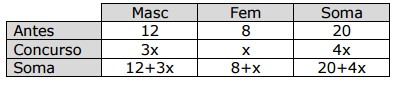
Calculando agora a probabilidade de escolhermos ao acaso um policial do sexo masculino, já sabendo pelo enunciado que essa probabilidade será de 0,7:
P = Espaço Particular / Espaço Amostral
0,7 = (12 + 3x) / (20 + 4x)
14 + 2,8x = 12 + 3x
0,2x = 2
x = 10
Assim, depois do novo concurso existirá um total de 10 + 8 = 18 policiais femininas.
Resposta: Certo.
-
Esclarecendo ainda mais a resolução do Yuri e Mozart, os 7/3 corresponde a 70% de homens (0.7) 30% de mulheres => 70/30 = 7/3
-
H=3M ( homens novos= 3 x mulheres novas )logo:
12+3M/20+4m=0,7
14+2,8M=12+3M
2=0,2M
M=2/0,2
M=10
Logo, mulheres que haviam antes = 8
Novatas=10
10+8= 18
errado
-
probabilidade= 12+3f / 20+4f = 7/10 --> 12 homens que já haviam + o triplo das fems que entraram / 20 total + total de novos policiais.
10(12+3f) = 7(20+4f)
--> 120+30f = 140+28f
--> 30f-28f = 140-120
-> 2f = 20
f=10 logo, policiais femininas que haviam 8 mais as novas 10, total =18.
-
Eu queria que alguem me dissesse se eu dei sorte pelo meu pensamento:
Homens = 3*Mulheres
Probabilidade de pegar Homem aleatoriamente = 0,7
Afirmação: "haverá mais de 15 mulheres?"
Se houverem pelo menos 15 mulheres, então 3*15= 45 homens
Logo para saber a probabilidade de pegar mulheres em relação aos homens ( se houver pelo menos 15 mulheres): 15/45 = 0,3 Mulheres
Entao, 1-0,3 = 0,7 é a probabilidade de se pegar homens.
Questao Correta
-
USEI O ENUNCIADO PARA RESOLVER ESTA QUESTÃO
SE CONTRATAR +8 MULHERES TEREMOS 16 AO TODO E AUTOMATICAMENTE +24 HOMENS
SOMANDO 36 HOMENS +16 MULHERES=52
36/52=0,69
OBS: SE 16 MULHERES É 0,69,ENTÃO PARA SER 0,7 SÃO MAIS DE 16 MULHERES
GABARITO:C
-
Galera, só uma dica: O Enunciado da questão(a amostragem) só serve para questão anterior. O problema efetivamente dado, já é o suficiente para resolução.
-
Usei o seguinte raciocínio: 0,7 é a probabilidade de se escolher o sexo masculino e o total é 60, levando em conta que 15 feminino e 3 vezes para o masculino é igual a 45. Multipliquei 0,7 por 60 que é igual a 42. Depois subtraí 60-42= 18. Portanto gabarito correto.
-
Vou tentar colocar a equaçao aqui, assim como costumava fazer no meu curso de engenharia:
Dando nome aos bois:
M= qtd de policiais masculinos, F= qtde policiais femininos
A quantidade total de policiais após a entrada de M policiais masculinos e F policiais feminos ficaria
20 + M + F (eq. 1), como o enunciado disse que a qtde nova de policiais masculinos era 3x a qtde de policias femino, entao
M = 3*F, (eq. 2), substituindo a eq, 2 em 1, ficará:
Qtde total de policiais (T) = 20 + 3F + F --> T = 20+4F
o enunciado tb diz que 0,7 é a probabilidade de se tirar 1 policial masculino do total, logo:
0,7 = (qtde de policial masculino antiga + novos)/total (T)
0.7 = (12+M)/(20+4F)
0.7=(12+3F)/(20+4F), desenvolvendo a equaçao achamos F=10, ou seja, entraram 10 novos policiais femininos,
logo ao somar a qtdade antiga com a nova temos: F`=8+10 = 18, gabarito CORRETO
-
montei uma equação 3.x+70=100
3x= -70 + 100
x= 30/3 = 10
10 + 8 mulheres existentes = 18
-
Fiz assim,
H = 12 + 3x - 70%
M = 8 + x - 30%
T = 20 + 4x - 100%
12 + 3x -------70%
20 + 4x --------100% Regra de três = (12+3x) . 100 = 70.(20+4x) Fazendo a conta da exatamente X=10
Substituindo M=8+x M = 8 + 10
Resultado M = 18
-
Se tiver mais de 15 como afirma a questão, tera no minimo16 mulheres.
Então 16 - 8 = 8 (novas mulheres)
novos homens = 3*8 = 24
24 + 12 = 36 = 0,69 ~ 0,7 como afirma a questão
todas as possibilidades 24 + 12 + 8 + 8
-
y = quantidade total de policiais (masculinos e femininos) após admissão
x = policiais femininas admitidas
3x = policiais masculinos admitidos
12 e 8 = policiais masculinos e femininos antes das admissões
(12 + 3x) + (8 + x) = y
y = 4x + 20
a probabilidade P de ser sorteado um policial masculino passou a ser 70%:
12 + 3x: total de policiais masculinos após a admissão
y = quantidade total de policiais (masculinos e femininos) após admissão
P = (12 + 3x) / y = 70/100
70y = 1200 + 300x
70 (4x + 20) = 1200 + 300x
280x + 1400 = 1200 + 300x
20x = 200
x = 10
(8 + x): total de policiais femininos após a admissão = 8 + 10 = 18
-
Acima de 15 (mulheres) = 16 mulheres
Antes eram 8 mulheres, entraram então + 8 = 16 mulheres
Quantidade de homes que entraram é o triplo de mulheres que entraram = 3x8 = 24 homens
Homens total = 12+24 = 36
Mulheres total= 8+8 = 16
Policiais totais = 52
P= casos favoráveis / casos possíveis
P = 36 / 52 = 0,7
-
Ótimo comentário Laudemir Martins.
-
"0,7 passe a ser a probabilidade de se escolher, ao acaso". Descordo completamente do Laudemir Martins, o CESPE pediu probabilidae 0,7 e não aproximadamente.
36/52 = 0.6923...
O calculo corretor seria, probabilidade atual de homem ao acaso 12/20
3x (n° de homens que entraram) e 4x (n° de pessoas que entrataram)
logo, 12 + 3x / 20 + 4x = 0,7
temos 12 + 3x = 14 + 2,8x => 0,2x = 2
x= 10
42h e 18m = 42/60 => exatamente 0,7
-
cespe às vezes aceita aproximação de valoresem outros momentos não, vai entender.
-
CORRETO
FAÇAM ESSAS DUAS EQUAÇÕES
X=HOMENS, Y=MULHERES
--X=3Y
--0,7= (12+X/12+X+8+Y)
Y=10, que somado com as 8 = 18
-
Questão que pode estar certa ou errada...CESPE sendo CESPE.
Se você colocar exatamente o número de 15 policiais do sexo feminino, da 0,73....
Se você colocar exatamente o número de 16 policiais do sexo feminino, da 0.6923...
E ai te pergunto, na gora da prova, valendo tua vaga na PF, o que tu marcas? Pois, se tu pegares a primeira situação e arredondar, TAMBÉM DA 0,7, se pegares a segunda situação, TAMBÉM DA 0,7.
Tenso!
-
Wagner Sigales, o enunciado afirma que os homens serão EXATAMENTE 70% do total de pessoas do batalhão. Com isso, a forma correta de se resolver irá nos levar a 18 mulheres e 42 homens. Resolver "chutando" valores não é a maneira correta, pode funcionar, mas não é a maneira correta. Portanto, nesse caso específico, o CESPE não errou
-
Batalhão: 20
H: 12
M: 8
Novos H: 3 * Novas M
P(H) = 0,7 = Novos H + 12 = 3*NovasM + 12 ----> NovasM = 10
Novos H + 20 + Novas M 3*NovasM + 20 + NovasM
10+8 = 18
CORRETO
-
jeito prático: Podemos confirmar a assertiva!!!
É dito que a nova probabilidade de escolhermos um homem ao acaso é 0.7.
A assertiva diz que então teremos um número de mulheres superior a 15.
Ora... Número de Homens = 3 x Número de Mulheres -------> Número de homens = 45
Dessa forma, 45/60(total, segundo a assertiva) = 0,75 que é diferente de 0,7.
Se aumentarmos em 3 o número de mulheres e diminuirmos em 3 o número de homens:
42/60= 0.7
R: C
-
-
Wagner Sigales, não viaja. Não vai precisar calcular nada disso.
Considera o nº de mulheres contratadas X e o nº de homens contratados 3X.
Jogando na fórmula P = Espaço Particular / Espaço Amostral vai chegar a:
7 / 10 (Probabilidade) = 12+3X (probabilidade de ser homem) / 20+4X (Total do batalhão)
7 / 10 = 12+3X / 20+4X
Resultando em X=10. Ou seja, foram contratadas 10 mulheres.
10 contratadas + 8 que já tinha = 18 mulheres no batalhão
-
fiz de uma maneira que considero mais simples, vejam se está correta:
48 (total)---100%
15 (M)------x
x=31...
Ou seja, para ser de 70% a probabilidade de ser um homem escolhido, precisa ter mais de 15 mulheres.
O que acham?
-
Aqui dá para aplicar o princípio da RATARIA
-
A questão está equivocada.
O item afirma que a quantidade dos policiais homens é 3x o numero das policiais mulheres.
Logo se a questão afirma maior de 15 teremos as seguintes possibilidades:
.
.
.
Opção A) Total de mulheres 15+1=16 (Mulheres antigas 8, Mulheres novas 8)
Total de homens= 3 x 8 mulheres novas = 24 Homens + 12 Homens = 36 Homens.
Logo teremos 36/52= 69,23%
.
.
.
Opção B) Total de mulheres 15+2= 17 (Mulheres antigas 8, Mulheres novas 9)
Total de homens= 3 x 9 mulheres novas = 27 Homens + 12 Homens = 39 homens
Logo teremos 39/56= 69,64%
.
.
.
Opção C) Total de Mulheres 15+3= 18 (Mulheres antigas 8, Mulheres novas 10)
Total de homens= 3 x 10 mulheres novas = 30 homens + 12 homens = 42 homens
Logo teremos 42/60= 70%.
.
.
.
.
A questão deveria mostrar 18 policiais mulheres ou mais de 17 policiais mulheres. Porque com 16 ou 17 policiais mulheres (o que é maior de 15) não deixaria a questão correta (69,63% e 69,64% respectivamente). Na minha humilde opinião!
-
o resultado não ser preciso e a banca dar uma resposta arredondada quebra todas as pernas do cidadão!!!
-

-
Fiz assim
3X + X = 70
4X = 70
X = 17,5
Arredonda para 18
Logo, Substitui o 18 no lugar do X na fórmula (3*18 = 54 e 1*18 = 18). Dessa maneira:
A Quantidade de mulheres é 18 e quantidade de homens é 54
-
Gostaria de saber, se realmente o "grande professor" Vinícius Verneck acha que alguem entende essa explicação que ele fez. Uma questão dessa, precisamos de uma explicação aprofundada, pois, não é simples e demanda um raciocínio maior. Reveja seus conceitos QCONCURSOS.
-
sangue de jesus tem poder
-
keila Viegas não é so você
-
já assisti a diversos vídeos de probabilidade e obsevei que o problema é a didática extremamente deficiente e ridícula dos professores, que dificulta e quase impossibilita principalmente para quem ainda está iniciando a matéria. identificar qual tipo de fórmula deve ser usado por exemplo, não vi um professor falar sobre isso. Surge a necessidade de fazer várias observações no material escrito porque não foi bem explicado, pensam que o aluno está dentro da mente deles e etc. simplesmente fazem o cálculo e pronto. Pronto, desabafei.
-
fiz assim pessoal
espero ajudar
12 + 3x = 0,7 T
8 + x = 0,3 T
onde T é o total de policiais
isolando o T
=> (12+3x)/0,7 = (8+x)/0,3 ou
=> (120 + 30x) /7 = (80 +10x)/3
=> 360 + 90x = 540 + 70x
=> 20x = 180 logo :
=> x = 9
como ja haviam 8 policiais feminias no batalhao soma a elas o x que da 8+9= 17
espero ter ajudado os amigos
-
A questão diz que dos que entraram, homens são o triplo das mulheres. Ou seja, a cada 3 homens, 1 mulher. E que a probabilidade de homens do total é de 0,7 (70%. ) Então, a cada 3 homens somados, somaremos uma mulher, até que o total de homens seja 70% do total de policiais.
H = 12 + 9 + 9 + 9 + 3 = 42
M = 8 + 3 + 3 + 3 + 1 = 18
H + M = 60
70% de 60 = 42
Então teremos + 15 (18) policiais mulheres
-
Calculando a probabilidade com 15 mulheres chegamos ao valor de 0,68
ou seja, o número de policiais femininas deve ser maior que 15 para obtermos P= 0,70
-
1º-NÚMERO DE POLICIAIS
Mulheres: 8 (antes do concurso) + x (acréscimo após o concurso): 8+x
Homens: 12 (antes do concurso) + 3x (triplo do acréscimo de mulheres após o concurso)
2º-PROBABILIDADE
Probabilidade de escolher um homem é igual ao evento escolher um homem (12 + 3x) sobre o espaço amostral (soma de 8+x e 12+3x, que fica 20+4x) que dará 0,7 (valor dado pela questão, que, em fração, equivale a 7/10). Fica assim: 12+3x/20+4x=7/10
3º-CÁLCULO
(1) 12+3x/20+4x=7/10. (2) Multiplique cruzado, que dará 120 + 30x = 140 + 28x. (3) Reorganize, ficando 30x-28=140x-120x, que resulta em 2x=20. X=20/2. x=10. Ou seja: o número de policiais mulheres que entrou após o concurso foi de 10.
4º- CONCLUSÃO
A questão quer saber se o total de mulheres após o concurso é maior que 15. Nós temos 8 (antes do concurso) + 10 (após o concurso). 8+10=18. 18>15. Questão CERTA.
-
Probabilidade coloca a autoestima no furico.
-
Antes:
12H e 8M total: 20
Após contratar novos policiais, onde o número de homens seja = ao triplo de mulheres:
Mulheres contratadas: 10
Homens Contratados: 10*3= 30
LOGO:
12 + 30H= 42
8 + 10M= 18 (18>15)
Gabarito: Certo
-
Resolução em vídeo
https://www.youtube.com/watch?v=8chuoyA3qk8
-
são 12 homens temos 3 vezes o nº de homens
08 mulheres temos x vezes o nº de mulheres
12 +3x= 70% são homens;
08 + x = 30% são mulheres;
são simplificados as porcetagem por 10.
3.(12+3x)= 7.(8 + x)
36 +9x= 56 + 7x
2x=20
x= 10, logo 08 mulheres + 10= 18 mulheres
------
@focopolicial190
-
Use o que a questão lhe oferece.
Se a questão diz que será mais de 15, faça o calculo com 15.
Com 15, supostamente, entraria 7 mulheres , logo, o tripo disso seria 21 e seria adicionado aos homens os quais ficariam: 12+21=33.
As mulheres + Os homens = 48 total
33/48 ,simplificando, daria 11/16.
11/16= 0,68.
Com isso daria para concluir que para ser 0,7 precisaria adicionar mais.
(Pense na forma simples de resolver, nem sempre muito calculo é sinal de inteligência.)
-
CERTO
Passo a passo de forma didática porque sei que muitos têm dificuldades nessa matéria:
No batalhão há:
12 homens
8 mulheres
Após o concurso:
+ 3x Homens
+ x Mulheres
Ele diz que após o novo efetivo, a possibilidade de escolher um homem é de 0,7 (ou seja 70%). Se a afirmação for verdadeira, então 30% são mulheres.
Homens = 12 + 3x = 70
Mulheres= 8 + X = 30
Vamos cortar os zeros do 70 e 30 e multiplicar cruzado. Fica assim:
3 . (12 + 3x) = 7 . (8 + x)
36 + 9x = 56 + 7x
7x - 9x = 56 - 36
2x = 20
x = 2/20
x = 10
Ou seja, entraram 10 mulheres. A questão diz que haverá mais de 15 mulheres. Está CERTO pois somando as novas (10) com as antigas (8) dá 18
-
Questão muito mal elaborada
-
12 + 3x (total do sexo masculino) dividido por 20 + 4x (total de pessoas) = 0,7
12 + 3x = 0,7 x (20 + 4x)
12 + 3x = 14 + 2,8x
3x - 2,8x = 14 - 12
0,2x = 2
x = 10
8 mulheres + x = 18 mulheres
12 homens + 3x = 42 homens
-
Calculando agora a probabilidade de escolhermos ao acaso um policial do sexo masculino, já sabendo pelo enunciado que essa probabilidade será de 0,7:
P = Espaço Particular / Espaço Amostral
0,7 = (12 + 3x) / (20 + 4x)
0,7.(20+4x) =12+3x
14 + 2,8x = 12 + 3x
-3x + 2,8x = 12-14
-0,2x = -2
X = -2 / -0,2
x = 10
-
Eu fiz o seguinte cálculo:
Considerando que 15 policiais são mulheres
Substitui com os resultados:
Antes eram 8 mulheres com agora serão 15:
15 - 8 = 7 novas mulheres
A questão fala que a quantidade de homens é o triplo da quantidade de mulheres
7 x 3 = 21
Antes eram 12 homens agora serão 33 :
Contudo, com as admissões a probabilidade de homens passa a ser 0,7 se escolher a ao acaso um policial que não seja mulher:
Agora utilizei a fórmula de probabilidade para os homens:
P = 33/48 = aproximadamente 0,68
Ou seja a quantidade de mulheres precisa ser maior que 15
GABARITO = CERTO
Fé todos os dias
Sonhos são reais
Nos vemos na posse
-
CERTO
Utilizando 16 mulheres no cálculo , que é superior aos 15 da suposição da questão...
Masc. = 36
Fem. = 16
36/52 = 0,69
se com 0,69 existem 16 mulheres, com 0,7 existem + ainda
-
questão Correta
ATRIBUAM UM VALOR MAIOR QUE 15 (QUALQUER VALOR) PARA AS MULHERES E FAÇA OS CÁLCULOS, MUITO MAIS FÁCIL
Supondo que o numero de mulheres admitidas seja, sei lá, 8 (pra dar 16 no total, somando com as 8 que já tinham), então o número de policiais do sexo masculino será 24 ( triplo de mulheres, como diz a questão).
somando a bagaça toda, depois do concurso, teremos um total de 52 policiais (12 + 24 homens, 8 + 8 mulheres = 36 + 16 = 52)
agora só faça o cálculo de probabilidade que a questão tá pedindo. Ela tá dizendo que se a probabilidade de escolher um homem for 70%, então depois de tudo terá mais de 15 policiais femininas no batalhão.
quando você fizer o cálculo de 36/52 (total de homens dividido pelo total de policiais), você vai achar um valor de 0,69, mais ou menos (69%).
Oras, se com 16 policiais femininas, que já é mais que 15, o número de policiais masculinos já está em 69%, é claro que com 70% o número de mulheres será maios que 15.
O número de policiais masculinos sempre será muito maior, pois o valor será 3x o numero de mulheres.
-
Use o que a questão lhe oferece.
Se a questão diz que será mais de 15, faça o calculo com 15.
Com 15, supostamente, entraria 7 mulheres , logo, o tripo disso seria 21 e seria adicionado aos homens os quais ficariam: 12+21=33.
As mulheres + Os homens = 48 total
33/48 ,simplificando, daria 11/16.
11/16= 0,68.
Com isso daria para concluir que para ser 0,7 precisaria adicionar mais.
(Pense na forma simples de resolver, nem sempre muito calculo é sinal de inteligência.)
-
Acerto a questão com o cálculo errado kk. Sério, não consigo entender como.
-
Gab: Certo
É importante atentar-se que o triplo não é do total, e sim dos novos.
Sendo assim, se considerarmos 15 mulheres, quer dizer que entraram 7 (Já havia 8, entraram 7 (8+7 = 15)).
Se entraram 7 mulheres, há o triplo de novos homens, que é igual a 21.
Nessa situação temos:
Homens: 21 novos + 12 antigos = 33
Mulheres: 7 novas + 8 antigas = 15
Total: 33 + 15 = 48
A probabilidade de escolher, ao acaso, um homem é de 33/48 = 0,69
Para aumentar essa probabilidade, eu teria que aumentar os homens. Para isso, aumento as mulheres também, pois a cada 1 mulher = 3 homens (triplo).
Concluindo, são mais de 15 mulheres.
Espero que ajude.
:D
-
Antes:
20 Policiais
12 homens = 12/20 = 0,6
8 mulheres = 8/20 = 0,4
Depois:
20 Policias + 3x (homens admitidos) + x (mulheres admitidas)
Note que: não sabemos, ainda, quantas pessoas foram admitidas, mas sim que foi três vezes maior o quantitativo de homens comparado ao das mulheres, por isso 3x e x
Agora então, teremos 20 policiais + 4x novos policiais, sendo 12 + 3x homens, e 8 + x mulheres.
A questão informa que a porcentagem de homens é 0,7
Então:
12+3x (quantidade de homens pós concurso) / 20 + 4x (total de policiais pós concurso) = 0,7
Basta resolver a equação.
Dica: Transforme o número decimal em fração, facilita na hora de fazer a conta, por mais que ela fique maior.
12+3x / 20+4x = 7/10
Multiplicando cruzado:
120 + 30x = 140 + 28x
30x - 28x = 140 - 120
2x = 20
x = 10
Agora basta substituir o X na quantidade de homens e/ou mulheres!
8 + x
8 + 10 = 18 mulheres
18 > 15
Reposta: CERTO
-
https://www.youtube.com/watch?v=8chuoyA3qk8
resolução do Prof Ivan Chagas
-
O Raciocínio que tive foi: Primeiro achar a Porcentagem do efetivo policial masculino 12/20 = 0,6 ou 60%. 70% = 0,7 (dado no enunciado) 70% de 20 = 14. Como o efetivo de policial Masculino no enunciado é o triplo multiplico: 14x3= 42 esse valor é o efetivo masculino após o concurso. Então faz regra de três para achar o valor de policiais do sexo feminino
42 - 70%
x - 30%
x=18 logo haverá mais do que 15 policiais do sexo feminino.
Gabarito: CERTO
-
Segui o seguinte raciocínio: tirar a prova da assertiva da questão. Segue o raciocínio.
Efetivo:
Masculino = 12
Feminino = 8
Total = 20
Com novas admissões:
Masculino = 12+3.X
Feminino = 8+X
Total: ?
Se a questão estiver certa, então ela diz que o feminino é Maior que o 15. Maior que 15 é a partir do 16. Supondo que o feminino seja 16, ficaria:
F=8+16=24
M=12+3.16=60
Total: 84
Após obter o resultado acima, efetua o seguinte cálculo:
60(Total de Masculinos)/84(Total de policiais)=0,7.
-
Compartilho o pensamento do professor Jhoni Zini:
Inicialmente possuímos 20 policiais: 12 homens e 8 mulheres.
12 homens
20 policiais
8 mulheres
Após o concurso, a quantidade dos novos policiais do sexo masculino admitidos foi igual ao triplo da quantidade de novos policiais do sexo feminino. Como não sabemos o valor das policiais feminias, atribuímos a variável x para ela, consequentemente, a quantidade de novos policiais homens será 3x.
12 homens + 3x
20 policiais Total de pessoas= 20 + 4x
8 mulheres + 2x
A questão afirma em seguida que a probabilidade de se escolher um homem é igual a 0,7, só com isso, conseguimos achar o total de homens, vamos para fórmula:
Probabilidade= Quantidade de homens/Total
0,7 = 12 + 3x / 20 + 4x
0,7 x (20 + 4x) = 12 + 3x
14 + 2,8x = 12 + 3x
14 - 12 = 3x - 2,8x
2= 0,2x
x= 10.
Não acabamos ainda, descobrimos apenas a quantidade de novas policiais admitidas ao batalhão, mas a questão pergunta a quantidade de mulheres no batalhão, observe abaixo:
12 homens + 3x -> 12 + 30 = 42 homens
20 policiais Total de policiais: 60
8 mulheres + x -> 8 + 10 = 18 mulheres
-
É só lembrar da fórmula da probabilidade: o que eu quero/total
Policiais MASC/TOTAL (fem e masc) = 0,7
Multiplica cruzado: 0,7 x total = masculino
e substitui:
0,7 x (12 + 3x) + (8 + x) = 12 + 3x
Acha o valor de x, que será 10 e depois substitui novamente para achar o total de policiais feminino e masculino.
-
Geralmente o pessoal reclama da resolução do professor por escrito. Mas nessa ele mandou bem
-
Vamos testar:
Antes do concurso: 12M + 8F
A questão afirma que terá mais de 15 femininas, então vamos testar com 15 no mínimo. Se antes tínhamos 8F então entrou mais 7F. Como entrou mais 7F então entrou o triplo masculino 21M.
Depois do concurso: 33M + 15F
Probabilidade de escolher um masculino: 33/48 = 0,68
Sendo assim, para uma probabilidade de 0,7 de escolher masculino certamente teremos mais do que 15 Femininas.
Gabarito CERTO.
-
Galera, vejam a resolução dessa questão no Canal Matemática com Morgado:
https://youtu.be/2WHkazoUP8Y
-
Gaste tempo em uma questão dessa correndo o risco de errar e perderá tempo para fazer outras que vão te aprovar.
-
Certo.
Fiz assim:
Caso sejam 15, entrariam mais 7 mulheres ( 8+7) = 15.
Novos policiais homens são o triplo das novas mulheres (7*3) = 21
O total, juntando com os antigos, ficaria 12 + 21 homens(33) e 15 mulheres = 48
Logo, pra escolher 1 homem, nessas condições seria 33/48 = 0,68.
Por isso, teriam que ser mais de 16 mulheres.