-
lâmbida tem média da uniforme = (2 + 4)/2 = 3 (isso mensal)
no período de 15 dias (que é igual a meio mês) o lâmbida será igual a 3*0,5 = 1,5Poisson = P(X=K) = e^-lâmbida*lâmbida^k / k!faça K = 2lâmbida = 1,5
-
λ=(2 + 4)/2 = 3 mensal, λ=3/2 quinzenal= 1,5
K=2
P= e^-λ . λ^k = e^-1,5. (1,5)^2= 0,22.2.25 = 0,2475= 24,75% Letra e)
K! 2! 2
-
Não entendi por que, fazendo com a média mensal(média 3, 4 ocorrências), o resultado deu diferente(16,25%).
Só acertei ao calcular com média 1,5 e 2 ocorrências(gabarito).
-
lambda = média mensal = 3 falhas
lambda = média quinzenal = 1,5 falhas
P(2) = (e^-1,5 * 1,5^2)/2!
P(2) = (0,22 * 2,25)/2*1
P(2) = 0,2475
-
A média de uma distribuição uniforme no intervalo [2, 4] é simplesmente (2+4)/2 = 3. Assim, em média temos 3 falhas por mês, de modo que em 15 dias (1/2 mês) é esperada a ocorrência de 1,5 falha. Portanto, temos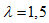 
. Para termos k = 2 falhas, a probabilidade da distribuição Poisson é:
Resposta: E
-
Questão boa!!! piscou, perdeu haha.
Vamos lá, seguem as dicas p vc não perder a questão como eu perdi:
1- encontre a média do intervalo pela fórmula da distribuição uniforme -> 4+2/2=3. Segundo o enunciado, esse valor é também o lâmbida MENSAL!!! (acaba sendo a média da distribuição de poisson tambémmm).
Ja temos a média mensal. ok. No entanto, a questão quer saber no período de 15 dias(metade do mês). A media será reduzida à metade, tambémmmm (=1,5)
2- a partir daí, basta utilizar a formula da distribuição de poisson, levando em consideração o EULER dado no enunciado; lâmbida sendo 1,5!!!!!!! e K=2 (conforme fornecido pelo enunciado). O resultado será a letra E.
Pessoal, estatística exige bastante treino. Sugiro que memorizem a formula da distribuição de poisson e tentem fazer a questão. BONS ESTUDOS!!!