-
temos que:
50% são formados em Administração: (A) = 50% ,
60% são formados em Ciências Contábeis: (C) = 60% ,
48% são formados em Economia (E) = 48% ,
Administração e Ciências Contábeis: (A ? C) = 20% ,
Administração e Economia: (A ? E) = 10% ,
Ciências Contábeis e Economia: (E ? C) = 30%
Pela teoria dos conjuntos temos que:
(A) U (C) U (E) = (A) + (C) + (E) - (A ? C) - (A ? E) - (E ? C) + (A ? E ? C)
Como (A) U (E) U (C) é a quantidade total de alunos, podemos dizer que é 100%
desta forma, (A ? E ? C) representa os auditores formados nos 03 cursos.
temos:
100% = 50% + 60% + 48% - 20% - 10% - 30% + A ? E ? C
A ? E ? C = 2%
assim podemos obter:
(A ? C) - 2% = 28%
(E ? C) - 2% = 8 %
O que buscamos é o nº de alunos que estudam pelo menos 2 disciplinas, 2 disciplinas ou 3 disciplinas.
Os nº dos que estudam 2 disciplinas é 18% + 28% + 8% = 54%
Os nº dos que estudam 3 disciplinas é 2%
Daí, o nº dos que estudam em pelo menos 2 disciplinas é 54% + 2% = 56%
-
Não compreendi de onde se chegou a conclusão desses 2% da junçao dos 3 grupos?
Please
-
Simples e objetivo...Valeu !!
-
Tirando a duvida da colega, os 2% sao referentes ao calculo
100% = 50% + 60% + 48% - 20% - 10% - 30% + A ? E ? C
100% = 158%-60%+A ? E ? C
100%= 98% + A ? E ? C
logo
A ? E ? C = 100%-98%
A ? E ? C = 2%
-
Pelo enunciado temos que:
* n(A) = 50% , n(B) = 60% , n(C) = 48% , n(AinterB) = 20% , n(AinterC) = 10% , n(BinterC) = 30%
Pela teoria dos conjuntos temos que:
n(AUBUC) = n(A) + n(B) + n(C) - n(AinterB) - n(AinterC) - n(BinterC) + n(AinterBinterC)
Como n(AUBUC) é a quantidade total de alunos, podemos dizer que é 100%
Daí,
100% = 50% + 60% + 48% - 20% - 10% - 30% + n(AinterBinterC)
n(AinterBinterC) = 2%
Desenhando o Diagrama de Venn podemos ver que, se n(AinterBinterC) = 2%, então n(AinterB) - 2% = 18%
, então n(AinterC) - 2% = 28%
, então n(BinterC) - 2% = 8 %
O que buscamos é o nº de alunos que estudam pelo menos 2 disciplinas, 2 disciplinas ou 3 disciplinas.
Os nº dos que estudam 2 disciplinas é 18% + 28% + 8% = 54%
Os nº dos que estudam 3 disciplinas é 2%
Daí, o nº dos que estudam em pelo menos 2 disciplinas é 54% + 2% = 56%
-
-
Não consegui entender porque se subtrai 2% e depois soma 2%? Alguém poderia me ajudar!?
-
so administração 50-20-10= 20
so contabeis 60-20-30= 10
so economia 48-10-30= 8
so um curso 20+10+8= 38
dois curso temos 10+20+30= 60
60+38= 98 ( isso equivale a 98% entao restam 2%)
100-98 = 2 esse dois fizeram os tres curso, então temos que diminuir 10,20 e 30 ou sena
10-2=8
20-2=18
30-2=28
somando os tres temos 54%, mais 2% que fizeram os 3 curso = 56% que a resposta s
fui entendido?
Fonte:http://www.soensino.com.br/foruns/viewtopic.php?f=5&t=12029
-
Uma outra maneira resolver a questão.
Na verdade uma forma desenvolvida da fórmula da teoria dos conjuntos.
Do diagrama temos
Total que tem Administração = 50
3 cursos = x
Administração+Contábeis = 20-x
Administração+Economia = 10-x
Só administração = 50 - (20-x) - (10-x) +x
Só administração = 20 + x
Total que tem Contábeis = 60
3 cursos = x
Contábeis+Economia = 30-x
Contábeis+Administração = 20-x
Só contábeis = 60 - (30-x) - (20-x) + x
Só contábeis = 10 + x
Total que tem Economia = 48
Economia+Contábeis = 30-x
Economia+Administração = 10-x
Só economia = 48 - (30-x) + (10-x) + x
Só economia = 8 + x
Logo,
Só 1 curso = 20+x+10+x+8+x = 38+3x
2 cursos = (30-x) + (20-x) + (10-x)
2 cursos = 60-3x
3 cursos = x
Então, igualando a 100%
100= 1 curso + 2 cursos + 3 cursos
100 = (38+3x)+(60-3x)+x
100 - 98 = x
x= 2
Então
Administração+Contábeis = 20-2 = 18
Administração+Economia= 10-2= 8
Economia+Contábeis= 30-2=28
Total de 2 cursos = 54
2 cursos+3 cursos = 54+2=56
É claro que com a fórmula é muito mais fácil e rápido!
Mas, para estudos, acredito que seja válido!
-
Não entendi porque somastes a intersecção dos 3 conjuntos em....
"(A) U (C) U (E) = (A) + (C) + (E) - (A ? C) - (A ? E) - (E ? C) + (A ? E ? C)"
Gostaria de saber o que é isso..ja que segundo a teoria dos conjuntos, a união de x conjuntos se dá a soma de seus nº de componentes, e a subtração das intersecções dos mesmos....por que está somando (A?E?C).?
PLZ...help me..!
-
O comentário da Catia esta ótimo, porém o sinal do "x" está errado.
Por exemplo em:
Só adm: 50 - (20 - x) - (10 - x) +x
Neste caso ao realizar a operção ficaria:
50 -20 + x - 10 + x + x
Que teria como resultado " 20 + 3x "
Corrigindo:
Só Adm.: 50 - (20 - x) - (10 - x) -x
50 - 10 + x - 20 - x - x
Só Adm.: 20 +x
Se eu estiver enganado me corriga.
Cometi o mesmo erro e fiquei meio confuso.
-
Segue uma melhor explicação que eu achei: http://www.bertolo.pro.br/UniubeSantaAdelia/Variedades/ConcursoBancoBrasil2010.pdf
Abraços,
-
Eu resolvi assim:
50+60+48-20-10-30 = 98
Quer dizer q 2% fazem os 3 cursos
Conjuntos:
2% na conexão dos 3 conjuntos
daí 18% fazem Adm e Contab, 28% Contab e Ec e 8% Adm e Ec
depois só completar: Adm falta 22 pra dar 50, Contab 12 para dar 60 e Ec 10 para dar 48
Que fazem 2 cursos: 18+8+28 = 54
3 cursos = 2
Total que fazem pelo menos 2 cursos: 56%
-
No enunciado diz de 20% adm e cont., 10% adm e ecom. e 30% cont e ecom. logo 20 +10+30= 60 % tem duas formação, então 40% tem só um a razão de 4 por 6 é 0,555... ou seja 56% pode ter duas formação
-
Tentando esclarecer a teoria dos conjuntos...
- As soluções propostas estão de acordo com a teoria quando afirmam que: n(AUBUC) = n(A) + n(B) + n(C) - n(AinterB) - n(AinterC) - n(BinterC) + n(AinterBinterC) ---> comentário de Everton e Aldir
- Essa formula é deduzida da própria teoria dos conjuntos: "a união de x conjuntos se dá a soma de seus nº de componentes, e a subtração das intersecções dos mesmos" (comentário de Carlos Eduardo Ferreira)
Trabalhando de dentro do conjunto para fora:
Demonstração da fórmula de acordo com a teoria (por partes): Vamos isolar as intersecções com se fossem três conjuntos, são eles:
X = A ∩ B
Y = A ∩ C
Z = B ∩ C, (dei nome aos conjuntos para facilitar)
sendo que a interseção entre esses conjuntos é A ∩ B ∩ C. Aplicando a teoria dos conjuntos, teremos:
n(X U Y U Z) = n(X) + n(Y) + n(Z) - n(A ∩ B ∩ C) ---> temos aqui a primeira fórmula.
Obs: se você não quiser substituir pelas letras X, Y e Z, a fórmula ficará desse modo:
n((A ∩ B) U (A ∩ C) U (B ∩ C)) = n(A ∩ B) + n(A ∩ C) + n(B ∩ C) - n(A ∩ B ∩ C)
Bom, agora temos que subir mais um nível, ous seja os conjuntos A (administrador), B (Ciências Contábeis) e C (Economia).
n(A U B U C) = n(A) + n(B) + n(C) - n(X U Y U Z)
PRONTO, agora basta substituir a expressão em destaque pela primeira fórmula e o resultado será:
parte 1: n(A U B U C) = n(A) + n(B) + n(C) - ( n(X) + n(Y) + n(Z) - n(A ∩ B ∩ C) )
parte 2: n(A U B U C) = n(A) + n(B) + n(C) - ( n(A ∩ B) + n(A ∩ C) + n(B ∩ C) - n(A ∩ B ∩ C) ) ---> substitui o X, Y e Z pelos valores originais.
parte 3: n(A U B U C) = n(A) + n(B) + n(C) - n(A ∩ B) - n(A ∩ C) - n( B ∩ C) + n(A ∩ B ∩ C)
Espero ter ajudado...
Bons Estudos \o/
-
A = 50%
C = 60%
E = 48%
A+C = 20%
A+E = 10%
C+E= 30%
x = interseção de A, C e E ( o espaço no meio dos conjuntos) = A+C+E
A + C + E - (A+C) - (A+E) - (C+E) + x = 100%
Para entender-mos melhor vamos isolar apenas o conjunto A:
A = 50% só que essa quantia é todo o conjunto A, incluindo as partes de A que fazem interseção com C, com E e com C e E ao mesmo tempo (x).
Ou seja, a parte do conjunto A que não faz interseção com nenhum outro conjunto é: 50 - (A+C) - (A+E) - (A+C+E).
Continuando a resolução da questão:
A + C + E - (A+C) - (A+E) - (C+E) + x = 100%
50 + 60 + 48 - 20 - 10 - 30 + x = 100
158 - 60 + x = 100
98 + x = 100
x = 2%
A questão quer saber a probabilidade do auditor ser formado em pelo menos 2 dos cursos. Primeiramente vamos separar cada interseção entre dois cursos da união entre os 3 (2%):
A+C= 20% - 2%= 18%
A+E= 10% - 2% = 8%
C+E = 30% - 2% = 28%
Agora é só somar as todas as interseções para saber a resposta:
(A+C) + (A+E) + (C+E) + x = 18 + 8 + 28 + 2 = 56%
Voltando ao exemplo do conjunto A, a porcentagem somente de A de auditores seria:
50 - (A+C) - (A+E) - x = 50 - 18 - 8 - 2 = 22
Se vocês fizerem isso com cada conjunto e depois somarem o valor de cada conjunto separado e cada interseção perceberão que dará 100% o resultado da soma.
Espero ter ajudado a quem não estava entendendo. =)
-
Se no enunciado da questão fala em "em pelo menos dois", não deveríamos considerar também os que são formados nos três cursos. Isso não implicaria num recurso ?
-
Esta
é uma questão clássica de Teoria dos Conjuntos e pode ser solucionada através
do Diagrama de Venn.
Inicialmente, para a confecção
do diagrama, insere-se as informações II, III e IV do enunciado.
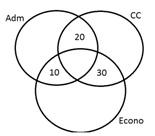
Posteriormente, insere-se as
informações escritas no item I, lembrando de subtrair os valores já presentes
no diagrama.
Dessa forma, considerando A, C,
e E, a porcentagem daqueles que fazem somente uma das disciplinas e T, aqueles
que fazem as três, tem-se:
A
+20+10 – T = 50
C
+ 20 + 30 – T = 60
E
+ 30 + 10 – T = 48
Assim,
A
– T = 20 → A = 20 + T
C
– T = 10 → C = 10 + T
E
– T = 8 → E = 8 + T
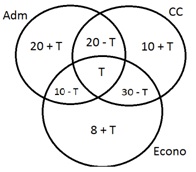
De acordo com os dados o
somatório dos campo é 100.
20+T+20-T
+10+T+10-T+T+30-T+8+T = 100
98
+ T = 100
T
= 2
Substituindo
os valores,
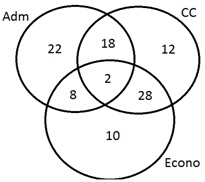
Finalmente,
a probabilidade de ele ser formado em pelo menos dois daqueles cursos citados
está destacado em amarelo.
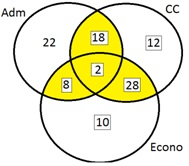
Assim, 18 + 2 + 8 + 28 = 56%
Resposta B
-
Eu entendi a resposta do colega acima, muito útil, por sinal. Como todos os funcionários são necessariamente formados, esses dois que sobraram são os que são formados nos três cursos. Por isso foram somados ao valor encontrado na soma que resultou nos 54 que são formados em dois cursos. muito legal e explicativo.
-
O raciocínio do Igor está COMPLETAMENTE errado.... Acertou a resposta por pura sorte.
Se as porcentagens de somente um fossem só aquelas (38%) a resposta seria 62% na resolução dele.
Em nenhum momento a questão cita porcentagens de SÓ dois cursos.
Essa questão sai facilmente por diagrama de VENN onde vc chama a interseção (que faz os 3 cursos) de x.
Você pode ver a resolução aqui: http://osmarmatematica.blogspot.com.br/2011_07_01_archive.html
Se a questão citasse porcentagens de APENAS DOIS CURSOS, aí sim poderia fazer pela resolução do igor.
-
Soma tudo e divede por 3
-
Pessoal, alguém por favor?
Pq subtrair os 2% dos percentuais de quem faz dois cursos, sendo que o valor faz parte dos 100%? Não teríamos que somar os 2% a esses valores?
-
Duas soluções
https://www.youtube.com/watch?v=n7u00EQtTUE&index=6&list=PLnKPHtCKz1p48VSi9vuA14dNiUrjgheCx
-
Questão resolvida no vídeo abaixo
https://www.youtube.com/watch?v=jyiaFn5U3YQ
Bons estudos.