Questão 1892116

• Banca: FCC
• Órgão: TRF - 3ª REGIÃO
• Ano: 2016
• Provas: FCC - 2016 - TRF - 3ª REGIÃO - Técnico Judiciário - Edificações
• Disciplina: Engenharia Civil
• Assuntos: Topografia

Para a locação de obras é necessário conhecer as coordenadas dos vértices do terreno e da edificação, normalmente determinadas a partir da locação de uma poligonal topográfica. Em um levantamento topográfico, determina-se o azimute inicial no primeiro alinhamento da poligonal com o objetivo de orientar o levantamento. Em um levantamento de uma poligonal com os vértices A, B e C, são conhecidos o azimute entre o alinhamento A-B (Az_AB = 125°20’25’’) e o rumo entre os alinhamentos B e C (R_BC = 30°30’30’’ SO). O azimute entre os alinhamentos B e C (AZ_BC) é igual a

• A. 335°50’55’’.
• B. 155°50’55’’.
• C. 94°49’55’’.
• D. 305°20°25’’.
• E. 210°30’30’’.

Gabarito: E

Comentários

• Letra E
  3ºQuadrante(SO): Az=180 + Rumo

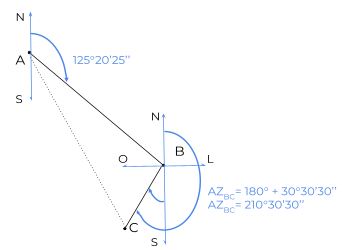
• Coordenada no 1º ponto:   A-B (AzAB = 125°20’25’’

  Cordenada no 2º ponto:   B e C (RBC = 30°30’30’’ SO)
  
  C = 30°30’30’’ -125°20’25’’

  
  Se C < 0

  
  Az = 30°30’30’ + 180 = 210º30'30''

• Apesar de toda historinha narrada no enunciado da questão e de dados que não desnecessários, a banca só queria saber se o candidato sabia realizar a conversão de rumo para azimute. 

   

  Como podemos ver, o alinhamento está no 3º quadrande (SO), logo o azimute é obtido por: 180º+R = 210º30'30"

• Explicando de uma maneira mais simples

  Azimute é o ângulo formado entre o NORTE de um ponto e o alinhamento (caminhamento) ao outro Ponto. Assim, o azimute de A para B só serve para locar o ponto B no circulo topográfico (circulo onde o giro é horário). O ponto B localiza-se no segundo quadrante (respeitando o giro horário);

  Rumo é o menor ângulo no eixo NS (Norte-Sul). o ângulo infomado para o Rumo BC significa que o ponto C está no terceiro quadrante (SO).

  Para encontrar o Azimute BC, basta somar 180º ao rumo BC.

   

• A questão exigiu conhecimento a respeito de noções de topografia. 
  
  Antes de resolver a questão, vamos relembrar os conceitos de azimute e rumo.
  
  O azimute é o ângulo medido a partir do NORTE no sentido horário até o alinhamento. Por outro lado, o rumo é o MENOR ângulo entre a direção considerada e a referência. A partir do norte ou do sul, variando de 0º a 90º (ver figura).
  
  
  
  Obs: As siglas W e E são as iniciais de oeste e leste em inglês.
  
  A partir dessa definições, vamos traçar a poligonal descrita na questão:
  
  
  • Azimute entre o alinhamento A-B (Az_AB = 125°20'25'') 
  
  
  
  
  • Rumo entre os alinhamentos B e C (R_BC = 30°30'30'' SO)
  
  
  
  A questão pede para encontrarmos o azimute entre B e C  (AZ_BC). Para encontrá-lo partiremos do norte no sentido horário (ver figura).
  
  
  
  Gabarito do Professor: Letra E.