-
Uma função linear é da forma y = ax + b, onde y é o valor do caminhão em função do ano de uso x.
A questão nos fornece dois pares ordenados: (0, 90000) e (4, 50000); e pergunta qual o vaor de y quando x = 2.
Precisamos achar os coeficientes da função.
Usando o primeiro par temos: 90000 = a.0 + b <=> b = 90000.
Usando o segundo par temos: 50000 = a.4 + 90000 <=> 4a = -40000 <=> a = -10000
Então a função fica assim: y = -10000x + 90000; aplicando x = 2 temos: y = -10000.2 + 90000 = 70000
-
percebe-se que a cada ano ele desvaloriza 10.000,00 com dois anos ele caio 20.000,00
90.000,00 - 20.000,00 = 70.000,00
-
se em falamos em 4 anos e depois em dois, cre-se que estamos falando no termo médio=
então
90.000 + 50.000 = 140.000/2 = 70.000.
-
Analisando o porquê da função limear: Quanto ao gráfico, b=0, pois a ordenada passa pela origem!
Agora uma relação importante quanto aos seus valores, e a relação com a variação proporcional:
"Duas grandezas são diretamente proporcionais quando ao aumentarmos o valor de uma delas um certo número de vezes, o respectivo valor da outra grandeza igualmente aumenta o mesmo número de vezes. Quando diminuímos o valor de uma delas, proporcionalmente o respectivo valor da outra também diminui"
Visto isso, uma função que estabelece entre x e y uma relação tal que y/x é constante é dita linear.
Expressamos a relação por y = a.x, "a" constante e dizemos que a variação de "y" é diretamente proporcional a variação de "x".
-
O problema pode ser resolvido por uma regra de 3 simples. Vejamos:
Se em 4 anos ele desvalorizou 40.000, quanto ele vai desvalorizar em dois anos?
40,000 --------- 4
X ---------- 2
4x = 40,000 x 2
4x = 80,000
x= 80,000/4
x= 20,000(valor da desvalorização em dois anos)
90.000(caminhão novo) - 20.000 = 70.000
-
A questão pode ser resolvida por matrizes, para isso, basta encontrar a equação da função.
Coloca-se os pares ordenados na matriz de terceira ordem, dessa forma;
0 90 1
4 50 1
x y 1
Após resolver a matriz pelo famoso método de Sarrus:
0 + 90x + 4y - 50x - 0 - 360 = 0
isolando o Y:
fica: y - 90 - 10x
Esta é a equação da função, a questão que saber qual é o valor de um caminhão do tipo A, com 2 anos de uso, em reais.
Basta colocar os 2 anos no lugar do X e calcular o Y.
y = 90 - 10 x 20 ==> y= 70
em reais: R$ 70.000,00
-
P1(0,90000)
P2 (4,50000)
Pela geometria analítica, calculamos a declividade ou coef.angular da reta;
m= 90000-50000/0-4 = -10.000
Pela equação abaixo definimos a função matemática; e escolhendo o Ponto 1 (P1) ao acaso;
y - yp= m (x-xp)
y-90000= -10000(x-0)
y- 90000=-10000x
f(x)=y= -10000x +90000
Substituindo x por 2 anos
y=-20000+90000
y= 70.000,00reais
-
De acordo com o enunciado, podemos construir a figura abaixo:
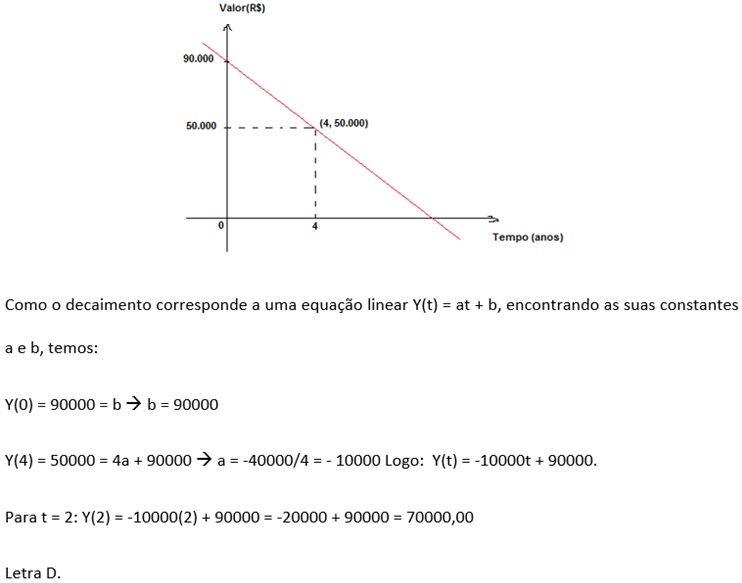
-
Espero que as questões na minha prova sejam nesse nível!! kkkkk
-
Seja “t” o tempo de uso de um caminhão e f(t) o preço deste caminhão, em função do tempo de uso. Foi dito que esta é uma função linear, ou seja, uma função de primeiro grau, do tipo: f(x) = ax + b. Ou melhor, usando a variável “t”:
f(t) = a.t + b
Sabemos que um caminhão novo (t = 0) tem preço f(0) = 90000. Ou seja,
f(0) = a.0 + b
90000 = b
Sabemos também que um caminhão com 4 anos de uso (t = 4) tem preço f(4) = 50000. Isto é:
f(4) = a.4 + b
50000 = 4a + 90000
-40000 = 4a
a = -10000
Portanto, temos a função linear que nos dá a relação entre o tempo de uso e o preço do caminhão:
f(t) = -10000t + 90000
Para t = 2 anos de uso, temos:
f(2) = -10000 x 2 + 90000 = 70000 reais
Resposta: D