Para começar vamos deduzir qual o grau do polinômio R(x).
Pela divisão euclidiana, podemos escrever P(x) como sendo:
P(x) = (x³-3x-1).Q(x) + R(x)
Ou seja, P(x) é o resultado da multiplicação de (x³-3x-1) por um quociente Q(x) desconhecido e somamos o resto R(x).
Sobre R(x), como o divisor (x³-3x-1) é um polinômio de grau 3, sobra apenas que o resto deve ter grau 2 ou menos. Portanto, R(x) é um polinômio de grau 2, grau 1 ou grau 0.
Observe que se descobrirmos que é P(x) resolvemos a questão. Então esse será o norte que seguiremos. Sabemos que ele tem todos os seus coeficientes inteiros.
Nosso problema dá uma raiz do polinômio P(x) que é (√2 + ³√3). Portanto, como
P(x) = x^6 + bx^5 +cx^4 + dx^3 + ex^2 + fx + g, temos que P(√2 + ³√3) será:
(√2 + ³√3)^6 + b(√2 + ³√3)^5 + c(√2 + ³√3)^4 + d(√2 + ³√3)^3 + e(√2 + ³√3)^2 + f(√2 + ³√3) + g
Vamos calcular termo a termo, separadamente:
x^6 = (√2 + ³√3)^6 , como se trata de algo do tipo (m + n)^6, com m=√2 e n=³√3 , temos
x^6 = m^6 + 6.m^5.n + 15.m^4.n^2 + 20.m^3.n^3 + 15.m^2.n^4 + 6.m.n^5 + n^6
Usando o mesmo raciocínio, calculamos os demais termos de P(x)
bx^5 = b(m^5 + 5.m^4.n + 10.m^3.n^2 + 10.m^2.n^3 + 5.m.n^4 + n^5)
cx^4 = c(m^4 + 4.m^3.n + 6.m^2.n^2 + 4.m.n^3 + n^4)
dx^3 = d(m^3 + 3.m^2.n + 3.m.n^2 + n^3)
ex^2 = e(m^2 + 2m.n + n^2)
fx = f(m+n)
g
Observe que m está elevado até a sexta potência e n também. Então, calcularemos cada um deles separadamente:
Agora, substituímos em cada um dos termos desenvolvidos.
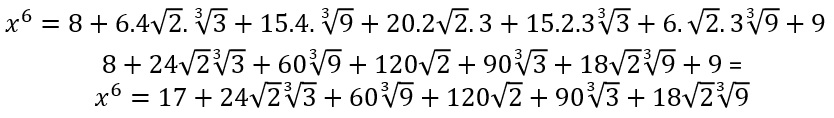
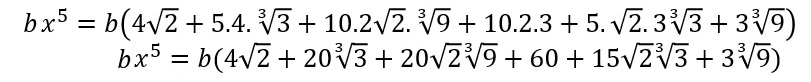
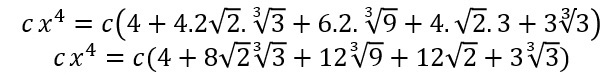
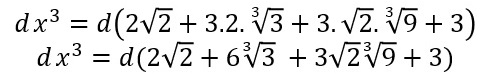
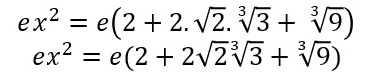
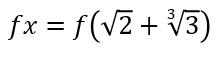
g
Agora iremos agrupar os termos semelhantes de todos os desenvolvimentos acima igualando a zero (pois aplicamos em x um valor que é raiz do polinômio)
* termos independentes:
17 + 60b + 4c + 3d + 2e + g = 0
-> 60b + 4c + 3d + 2e + 0f + 9 = -17
* termos com 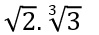
24 + 15b + 8c + 2e = 0
-> 15b + 8c + 0d + 2e + 0f + 0g = -24
* termos com 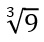
60 + 3b + 12c + e=0
-> 3b + 12c + 0d + e + 0f + 0g = -60
* termos com 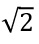
120 + 4b + 12c + 2d + f = 0
-> 4b + 12c + 2d + 0e + f + 0g = -120
* termos com 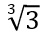
90 + 20b + 3c + 6d + f = 0
-> 20b + 3c + 6d + 0e + f + 0g = -90
* termos com 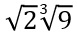
18 + 20b + 3d = 0
-> 20b + 0c + 3d + 0e + 0f + 0g = -18
Como termos 6 equações com 6 incógnitas, vamos resolver esse sistema linear utilizando matrizes.
Iremos somar linhas para zerar mais ainda as colunas.
(Vou usar a seguinte notação: ex: L8 -> L8 + 3L7 , lemos linha 8 se transforma em linha 8 mais 3 vezes linha 7)
Para ficar com f em apenas uma linha:
L5 ->L5 - L4
Agora, vamos zerar a coluna de e:
L1 -> L1 - 2L3
L2 -> L2 - 2L3
Observe as linhas 2, 5 e 6:
9b -16c + 0d = 96
16b -9c + 4d = 30
20b + 0c + 3d = -18
Ou seja, um novo sistema de 3 equações e 3 incógnitas, que resolveremos em matriz a parte:
L2 -> 3L2
L3 -> 4L3
L2 ->L2 - L3
L1 -> 27L1
L2 -> 16L2
L2 -> L2 - L1
Portanto, da linha 2, temos que -755b = 0, logo b=0
Substituindo b=0 nas demais, temos:
243.0 - 432c = 2592 -> c = -6
80.0 + 12d = -72 -> d = -6
Voltando à matriz completa descobriremos as demais incógnitas:
54.0 -20.(-6) + 3.(-6) + g = 103
120 -18 + g = 103 -> g=1
3.0 + 12(-6) + e = -60
-72 + e = -60 -> e = 12
4.0 + 12(-6) + 2(-6) + f = -120
-72 -12 + f = -120 -> f = -36
Logo, P(x) = x^6 + 0x^5 -6x^4 -6x^3 + 12x^2 - 36x + 1
Agora, vamos dividir P(x) por x³ - 3x -1
Como o grau 2 é menor que o 3 do divisor, então paramos a divisão e temos que R(x) = 3x² - 54x - 4
Somando os coeficientes de R(x):
3 + (-54) + (-4) = -55.
Logo, temos a resposta na Letra E: -55
Gabarito do Professor: Letra E.