-
Temos:
Ds= Densidade aparente seco; Dr=Densidade real; n=Porosidade
Ps= Peso do sólido Vt= Volume total Vv= Volume de vazios Vs= Volume dos sólidos
Ds= Ps/Vt Dr= Ps/Vs n= Vv/Vt Vv= Vt - Vs
Ds*Vt = Dr*Vs ---> Ds/Dr = Vs / Vt ---> Ds/Dr = [( Vt -Vv)/Vt]
Ds/Dr = 1 - n ---> n = 1 - Ds/Dr ---> n = 1 - 2,0/2,5 ---> n = 0,2
-
Damião, me tira uma dúvida!
A densidade do sólido não seria Ds = Peso de sólido / volume de sólido, e a Densidade Real não seria Dr = Volume total / Volume total
Peso total = Peso Sólidos + Peso de Líquido por exemplo.
Fiquei na dúvida, se possível me dê uma ajuda!
Abraço!
-
Nao junior, a densidade sempre vai ser massa sobre volume!
-
Porosidade : VV/VT
= (0,5/2,5) = 0,2
-
A Densidade Real de solos é a relação entre o peso específico das partículas sólidas (
-
Pra resolver essa questão tem que considerar que a "densidade real" é o peso específico aparente seco (Ps/Vt) e a "densidade real da parte sólida" é o peso específico real (Ps/Vs). Nunca ouvi falar em "densidade real" e "densidade real da parte sólida"... pra mim "real" se relaciona unicamente com volume seco. Deveriam então ter usado densidade aparente e densidade real, já que queriam inovar nas palavras...
-
2,5 = Ms/Vs -> Ms = 2,5*Vs (I)
2,0 = Ms/Vt -> Ms = 2,0*Vt (II)
Igualando as equações I e II:
2,5Vs = 2Vt
Como Vs = Vt - Vv:
2,5(Vt - Vv) = 2 Vt
2,5Vt - 2,5Vv = 2Vt
0,5Vt = 2,5Vv
Vv/Vt = 0,5/2,5 =0,2
-
amostra_porosa 2,50 ---- 100%
amostra_solida 2,00 --- x
x = 80% de sólido
20% de porosidade
-
Primeiramente, é
importante definir que a porosidade (n) é um índice físico que expressa
a relação entre o volume de vazios (Vv) e o volume total da
amostra (Vt), isto é:
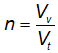
Por sua vez, a densidade
(ρ) trata-se da relação entre a massa (m) e o volume (V) de um corpo. Visto
isso, a densidade real (ρr) de uma amostra de solo consiste
na relação entre a massa dos sólidos (ms) da amostra e o volume dos
sólidos (Vs); enquanto a densidade da parte sólida (ρs)
equivale ao quociente entre a massa dos sólidos (ms) da amostra e o
volume total (Vt). Visto isso, pode-se escrever que:
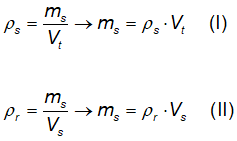
Relacionando as equações
(I) e (II) e dado que o volume de sólidos (Vs) é igual a
diferença entre o volume total (Vt) e o volume de vazios (Vv),
resulta que:
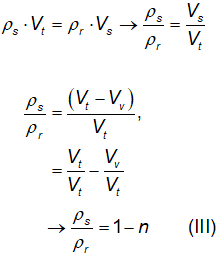
Reescrevendo a equação
(III) com a porosidade em evidência, encontra-se a seguinte relação:
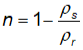
Por fim, de acordo com os
dados do enunciado (ρs = 2,00 e ρr = 2,50), pode-se
calcular a porosidade:
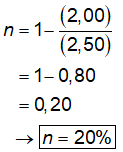
Portanto, a porosidade
do solo da amostra do problema é igual a 20%. Assim, a alternativa E
está correta.
Gabarito do Professor: Letra E.