-
− Carga do pilar: 1200 kN
− Taxa admissível do solo: 0,30 MPa
Área da Sapata = 1200 kN/ 300kPa
A = 4m²
Se a área é igual a 4m², pode dimensionar uma sapata quadrada de lado igual a 2m.
"Calma, calma! Eu estou aqui!"
-
GABARITO: D
Ye lê lê, mais uma questão de fundações que desconhece o teor da NBR 6122.
Quais outras questões vacilaram, que eu lembre agora? Q698017, Q784027
Copiando texto próprio meu de uma dessas questões, vislumbrando aquilo que a presente questão se negou a ver, da NBR supra:
5.6 Peso próprio das fundações
Deve ser considerado o peso próprio de blocos de coroamento ou sapatas ou no mínimo 5 % da carga vertical permanente.
Tenho seriamente dúvidas acerca do que eu faria caso caísse uma questão dessas em concurso que eu preste e preze. Creio que eu marcaria a opção tecnicamente correta (mesmo esperando gabarito divergente) e iria brigar a alteração do gabarito. Considero razoável a chance de que ganhasse a questão e, principalmente, de, assim, melhorar minha classificação.
Voltando à presente questão: a carga atuante é 1200*1,05 kN, de forma que a área mínima da sapata deve ser de 1200*1,05/300m² = 4,2m², de sorte que a alternativa tecnicamente correta é a A, pois B, C e D não atendem à "taxa admissível do solo", e alternativa E é excessivamente grande.
-
Eu partilho da opnião do colega Guilherme Rayol. Infelizmente a banca não considerou algo importante da norma para a questão.
A resposta correta teria que ser uma sapata de no mínimo 2m x 2,2m.
-
Perfeito comentário Guilherme, como sempre agregando conhecimento aos colegas do QC. Obrigado!
-
Alonso nos ensin que devemos multipplicar 1,05 (5%) para carga. a FCC desconhece isso.
-
DIRETRIZES PARA A ESCOLHA DAS DIMENSÕES a e b da sapata.
● Centro de gravidade da sapata → coincidir com o do pilar;
● Nenhuma dimensão menor que 60 cm;
● Relação entre os lados a e b menor ou igual a 2,5;
● Balanços em relação as faces do pilar iguais nas duas direções.
-
P = F/A
300 (KPa) = 1200 (KN) / A
A = 1200 (KN) / 300 (KPa)
A = 4 m²
lado = 2m
-
A sapata
trata-se de um elemento de fundação superficial caracterizado por transmitir
os esforços para o solo pela sua base. Visto isso, a área da base de uma
sapata é calculada por meio da seguinte equação:

Em que A é a área da base
da sapata; P a carga do pilar; e σadm a tensão (ou taxa) admissível
do solo. Lembrando que 1 MPa =
1.000 kN/m², resulta que:
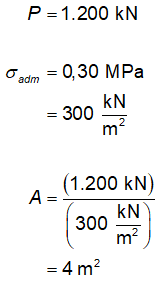
A forma mais
econômica da sapata é aquela com dimensões proporcionais às do pilar. Dado que o pilar é quadrado, a sapata
mais econômica também é quadrada. Sendo L o lado da sapata quadrada, e
lembrando que a área da sapata é L·L, tem-se que:
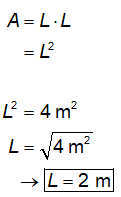
Portanto, a forma
mais econômica da sapata do problema é quadrada de lado 2 m. Logo, a
alternativa D está correta.
Gabarito do professor: letra
D.