-
CERTO.
A função de utilidade apresentada, u(x, y) = ax + by (a=5; b=2), é de bens substitutos perfeitos (a taxa marginal de substituição é constante), neste caso existem três escolhas ótimas possíveis:
1) Se preço de y > preço de x, a inclinação da reta orçamentária será mais plana do que a curva de indiferença. Nesse caso, a cesta ótima será aquela em que o consumidor gastar todo o seu dinheiro no bem x.
2) Se preço de x > preço de y, o consumidor comprará apenas o bem y.
3) Se preço de x = preço de y, haverá todo um segmento de escolhas ótimas, neste caso todas as quantidades dos bens x e y que satisfizerem a restrição orçamentária serão uma escolha ótima.
Portanto,
No caso da questão, se o preço de x (200 UM) é maior que o preço de y (50 UM), temos a hipótese 2. Se a renda = 1000, e o João irá gastar toda sua renda com o bem y (x = 0), então quantidade demandada será igual ao quociente da renda e o preço do bem, ou seja, 1000/50 = 20 unidades do bem y. Assim, João irá demandar 20 unidades do bem y e nenhuma unidade do bem x.
-
Como eu fiz:
Joguei na fórmula...
João: u(x, y) = 5(1) + 2(0) = 5 utilidades (limitada ao orçamento de R$1.000,00)
João: u(x, y) = 5(0) + 2(20) = 40 utilidades (limitada ao orçamento de R$1.000,00)
Logo podemos concluir que o nível de utilidade é muito maior em consumir apenas itens Y e sacrificar os itens X.
Abraço!
-
Com 1000 reais ele pode comprar : 5 unidades do bem X OU 20 unidades do bem Y OU uma combinação entre eles , ex : 2 unidades de X , 12 unidades do bem Y.
Sabendo que joão é racional , ele vai escolher a combinação que resulta em maior satisfação . Ai vc tentaria as opções e encontraria que se ele comprasse apenas o bem y, teria 40 de utilidade, se fosse só o bem x = 25 de utilidade e por ai vai.
Mas se vc soubesse que a função em tela é de substitutos perfeitos, saberia que o consumidor escolhe o produto mais barato, e que a maior quantidade em regra resulta uma utilidade maior.
-
GABARITO :CORRETO
Reta de restrição orçamentaria = conjunto de todas as cestas que exaurem a renda do consumidor
Escolha Otima do consumidor = combinação de produtos que maximiza a UTILIDADE, o consumidor atinge o limite da sua reta de restrição orçamentaria. a curva de indiferença(TMGS) estará tangenciando a RETA ORÇAMENTARIA,
A Questão disse:
Restrição Orçamentaria é = $1000
BEM Y = $50
( vc tem que ver a qtd do bem Y que vai dar igual a $1000, isso é a 'escolha otima' , ' maximizar utilidade' )
$50 x 20 = $ 1000
obs: se esse consumidor quiser consumir alguma quantidade do BEM X, ele tera que reduzir o consumo do bem Y
-
Apenas um breve ajuste e complementação na resolução do nobre colega Wagner Sigales:
João: u(x, y) = 5(5) + 2(0) = 25 utilidades (limitada ao orçamento de R$1.000,00), tendo em vista que poderíamos comprar 5 unidades do bem "x", com tal restrição orçamentária.
João: u(x, y) = 5(0) + 2(20) = 40 utilidades (limitada ao orçamento de R$1.000,00), comprando 20 unidades do bem "y".
Sabendo que os bens são substitutos perfeitos, não precisa se falar em combinação de bens.
Bons estudos.
-
m >= p1.q1 + p2.q2
João: u(x, y) = 5x + 2y (Função 1 grau / reta)
R$ 50,00 * 20 unid. y = 1.000 (Restrição orçamentária)
Para demandar alguma qtde do bem x, terá que reduzir a qtde do bem y (Assim, ficará dentro da R.O)
-
Quando se trata de bens substitutos perfeitos, o consumidor sempre preferirá comprar o bem mais barato, aumentando a utilidade!!!!
Vendo a curva de utlidade, pode-se notar que se trata de uma reta. Assim, são bens substitutos perfeitos.
-
X > Y, todo o dinheiro será gasto no bem Y;
X < Y, todo o dinheiro será gasto no bem Y;
X = Y, escolha ótima.
Não desiste!
-
Agora, a questão nos deu dados para calcular a restrição orçamentária do consumidor e vermos qual será o ponto em que o consumidor extrairá mais utilidade (o equilíbrio do consumidor).
Bom, como estamos diante de bens substitutos, nós teremos uma solução de canto. Olhe só:
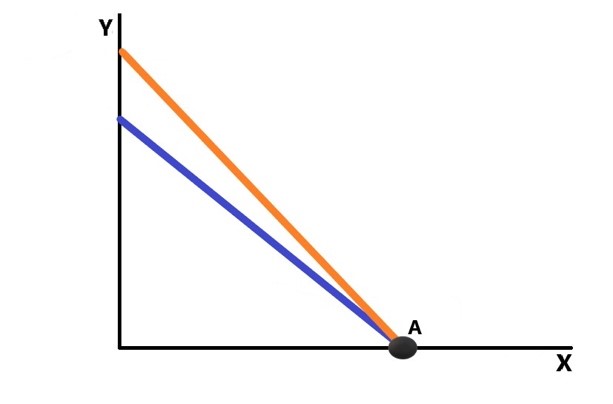
A reta laranja é a curva de indiferença de um consumidor qualquer (como a função utilidade é do tipo U = aX + bY, a curva de indiferença é uma reta). Já a curva azul é a restrição orçamentária desse consumidor.
Para que esse consumidor atinja o máximo de utilidade, é necessário que ele toque a curva de indiferença mais alta. E isso ocorre justamente no ponto A acima.
Agora, vamos pensar no caso do João. João também apresenta uma função utilidade do tipo U = aX + bY . Por isso, também teremos uma curva de indiferença reta e uma solução de canto. Isso acontece porque a curva de indiferença (“reta de indiferença”, rsrsrsrs) não tangencia a linha do orçamento, mas encosta nela num dos cantos.
Em toda solução de canto, o consumidor irá concentrar seu consumo no bem que tiver uma boa relação entre o preço que ele paga e a utilidade que ele recebe. No caso de João, ele irá concentrar seu consumo naquele bem cuja utilidade ponderada pelo preço seja maior.
Explicamos!
A função utilidade de João é U = 5x + 2y. Pela função de utilidade, note que cada unidade do bem X proporciona “5” de utilidade para João, ao passo que cada unidade do bem Y proporciona 2.
Ou seja, uma unidade do bem X proporciona 2,5 mais utilidade do que uma unidade do bem Y (só dividir 5 por 2).
Acontece que o preço do bem X é 200 e o preço do bem y é 50. Ou seja, o preço do bem x é 4 vezes maior. Olhe só que interessante: o bem x custa 4 vezes mais, mas apresenta apenas 2,5 vezes mais utilidade. Não é uma boa relação custo benefício. Por isso, João não obterá o máximo de utilidade consumindo o bem x.
Na verdade, como os bens são substitutos perfeitos, João terá máxima utilidade comprando tudo que puder de Y e nada de X. Isso acontece porque como o bem x tem uma relação ruim, é melhor para João gastar tudo com Y, o que nos fará chegar a nossa solução de canto.
Como João vai gastar tudo com o bem Y, basta dividirmos a renda de João pelo preço do bem Y e teremos a quantidade demandada deste bem:
Resposta: C
-
Fala pessoal! Tudo beleza? Professor Jetro Coutinho na área, para comentar esta questão sobre Teoria do Consumidor!
A questão nos deu dados para calcular a restrição
orçamentária do consumidor e vermos qual será o ponto em que o consumidor
extrairá mais utilidade (o equilíbrio do consumidor).
João possui a função de utilidade 5x + 2y, o que significa que, para João, os bens x e y são substitutos. Bom,
como estamos diante de bens substitutos, nós teremos uma solução de canto. Olhe
só:

A reta laranja é a curva de
indiferença de um consumidor qualquer (como a função utilidade é do tipo U = aX
+ bY, a curva de indiferença é uma reta).
Já a curva azul é a restrição orçamentária desse consumidor.
Para
que esse consumidor atinja o máximo de utilidade, é necessário que ele toque a
curva de indiferença mais alta. E isso ocorre justamente no ponto A acima.
Agora,
vamos pensar no caso do João. João também apresenta uma função utilidade do
tipo U = aX + bY . Por isso, também teremos uma curva de indiferença reta e uma
solução de canto. Isso acontece porque a curva de indiferença (“reta de
indiferença", rsrsrsrs) não tangencia a linha do orçamento, mas encosta nela num
dos cantos.
Em
toda solução de canto, o consumidor irá concentrar seu consumo no bem que tiver
uma boa relação entre o preço que ele paga e a utilidade que ele recebe. No
caso de João, ele irá concentrar seu consumo naquele bem cuja utilidade
ponderada pelo preço seja maior.
Explicamos!
A
função utilidade de João é U = 5x + 2y. Pela função de utilidade, note que cada
unidade do bem X proporciona “5" de utilidade para João, ao passo que cada
unidade do bem Y proporciona 2.
Ou
seja, uma unidade do bem X proporciona 2,5 mais utilidade do que uma unidade do
bem Y (só dividir 5 por 2).
Acontece
que o preço do bem X é 200 e o preço do bem y é 50. Ou seja, o preço do bem x é
4 vezes maior. Olhe só que interessante: o bem x custa 4 vezes mais, mas
apresenta apenas 2,5 vezes mais utilidade. Não é uma boa relação custo
benefício. Por isso, João não obterá o máximo de utilidade consumindo o bem
x.
Na
verdade, como os bens são substitutos perfeitos, João terá máxima utilidade
comprando tudo que puder de Y e nada de X. Isso acontece porque como o bem x
tem uma relação ruim, é melhor para João gastar tudo com Y, o que nos fará
chegar a nossa solução de canto.
Como
João vai gastar tudo com o bem Y, basta dividirmos a renda de João pelo preço
do bem Y e teremos a quantidade demandada deste bem:
Y = R/Py
Y = 1000/50 = 20
Gabarito do Professor: CERTO.