Questão Q874425

Na economia formada pelos consumidores João, Pedro e José, observam-se as seguintes funções utilidade com relação aos bens x e y:

João: u(x, y) = 5x + 2y;

Pedro: u(x, y) = 3x + 2y;

José: u(x, y) = 5x² + 2xy + 0,8y² .

Em relação a essa economia, julgue o item a seguir.

A função utilidade de Pedro é côncava.

Alternativas

Certo

Errado

Comentários

Como assim? A função de pedro é uma RETA ¬¬
também não entendi.... se alguém puder explicar......
O CESPE considerou o item como correto mesmo depois dos recursos.

No entanto, a função de utilidade de Pedro é linear e não côncava.

Um teste para avaliar se a função é côncava é verificar se a derivada segunda da função é negativa, o que não é o caso, pois a derivada segunda da função utilidade de Pedro é igual a zero.

Vamos indicar para comentário do Professor.
Essa foi boa, acho que alguém importante ficou por uma questão, ai resolveram mudar o gab. Não tem explicação lógica para dizer que a utilidade de uma função de bens substitutos perfeitos seja concava. Indiquem para o comentário !
GABARITO: CORRETO

Quando o consumidor consome APENAS 1 BEM, a função de utilidade é CONCOVA , e a tmgs é crescente.
Tá errado isso aí.

Pra ser côncava a função tinha que ser algo parecido com U(x1,x2) = x1x2
U(x,y) = 3x + 2y

X Y U

0 20 40

1 16 35

2 12 30

3 8 25

4 4 20

5 0 15

Variação constante da utilidade, logo como ela poderia ser côncava?

função linear.
No caso dos chamados bens substitutos perfeitos , a curva de indiferença apresenta a forma de uma reta negativamente inclinada.
Cespe sendo Cespe...
Entendi nada, a função é linear .

Questão Errada
A única explicação plausível é que em curvas de indiferenças côncavas a preferência é pela especialização do consumo, seria uma solução de canto.

Também fiquei em dúvida, vamos esperar o comentário do professor.
Por favor,

Indiqem a questão pra comentário, pois os colegas não conseguiram chegar a uma explicação taxativa.
O enuciado da questão fala sobre a FUNCÃO UTILIDADE. Logo deve-se considerar o UTILIDADE dos produtos para Pedro.
Vou utilizar a tabela do nosso amigo P torezani :

U(x,y) = 3x + 2y

X Y U

0 20 40

1 16 35

2 12 30

3 8 25

4 4 20

5 0 15

Percebe-se que o maior nível de satisfacão (utilidade) para Pedro será ao consumir apenas o Y (utilidade 40) .Sendo assim quando existe prefêrencia pela ESPECIALIZACÃO no consumo, a curva será CÔNCAVA.
Um consumidor com preferências estritamente côncavas entre dois bens, especializa-se no consumo de um deles. No limite, o consumidor ira maximizar sua utilidade quando consumir todas as suas possibilidades em apenas um bem. Solução de Canto.
A função utilidade de Pedro é côncava.

Pessoal, quando a questão afirma isto, ela se refere que a todo instante a curva será côncava. A questão está errada, uma reta não pode ser côncava, é uma reta.

Teve uma questão que a CESPE disse que a curva de indiferença é usualmente CÔNCAVA, Quando na verdade ela é USUALMENTE CONVEXA.

A PERGUNTA É: QUEM ELABORA ESTAS QUESTÕES?
y = ax + b (LINEAR)
Toda função afim é Homogênea, Côncava e Convexa. Gabarito CERTO!
Fala pessoal! Professor Jetro na área!

Esta questão trata do conteúdo de Teoria do Consumidor da Economia. Para responder a questão, além de reconhecer o padrão da função utilidade, é necessário conhecer um conceito matemático. Podemos até dizer que é uma questão que cobra mais Matemática do que Economia em si.

Bom, na Teoria do Consumidor, temos várias funções utilidade, que representam as preferências do consumidor. Quando temos bens substitutos, o formato da função utilidade é o seguinte: U (X,Y) = a.X + b.Y.

Esse tipo de função utilidade representa uma curva de indiferença linear, como no gráfico abaixo (de elaboração própria):

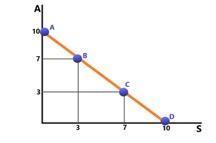
A curva de Pedro segue exatamente o mesmo formato (3x +2y), o que denota que, para Pedro, os bens X e Y são substitutos.

Bom, como a função utilidade de Pedro segue o formato da função utilidade para bens substitutos, teremos uma curva de indiferença linear, seguindo a regra.

E aí, vem o grande “embaraço" da questão, pois o concurseiro pode pensar assim: "se a curva de indiferença é linear, ela não pode ser côncava e, portanto, questão errada."

Mas na verdade não é assim. Neste momento é que entra o tal conceito matemático envolvido, que é crucial para o acerto da questão.

Apesar de não caber a demonstração aqui, segundo a Matemática, curvas lineares (retas) são ao mesmo tempo côncavas E convexas. Ou seja, as curvas de indiferença para bens substitutos, que são curvas lineares, são consideradas simultaneamente côncavas e convexas.

Portanto, como a função utilidade de Pedro representa uma curva de indiferença linear, esta curva é considerada tanto côncava quanto convexa, o que nos permite julgar a questão como CERTA.

"Mas professor, preciso me preocupar com questões desse tipo na minha prova?" Bom, a resposta é 'depende". Esta prova da ABIN foi uma prova específica para Economistas, profissionais que já na sua formação apreendem alta carga em matemática. Por isso, é razoável a banca cobrar esse tipo de conhecimento em provas específicas para Bacharéis em Economia.

Diferentemente, se o concurso para o qual você está estudando não é exclusivo para bacharéis em Economia, a probabilidade de cair uma questão dessas diminui drasticamente.

Seja como for, agora você já está preparado caso haja cobrança de uma questão semelhante.

Gabarito do professor: CERTO.
Resumindo o comentário do professor,
Segundo a Matemática, curvas lineares (retas) são ao mesmo tempo côncavas E convexas. Ou seja, as curvas de indiferença para bens substitutos, que são curvas lineares, são consideradas simultaneamente côncavas e convexas.

SóProvas

Continue usando...

O que está incluso