-
Slutsky ensina o seguinte, Efeito total = Efeito renda + Efeito substituição. O Efeito substituição = variação na demanda dos bens trocados.
Situação Anterior : Ele tinha uma renda de 100, capaz de comprar 50 unidades de X ou 10 unidades de Y ou combinações. Dado que o preço de X=2 e Y=10. Quando tem uma variação nos preços , há uma variação na restrição orçamentária, agora com o novo preço de X=5, o consumidor só consegue comprar 20 unidades de X ou 10 unidades de Y ou combinações
Para calcular, slutsky ensima : Efeito substituição = Demanda com renda compensada e novo preço ( ???) - Demanda inicial
Para calcular a demanda da renda compensada, Slutsky ensina o seguinte, fazemos uma compensação na renda de modo a consumir exatamente o que podia antes, respeitando os novos preços. Ou seja, quanto é necessário para consumir 50 unidades de X e 10 unidades de Y, sabendo que o novo preço de X=5. Renda Compensada = 50 * 5 + 10 * 10 = 250 ,como ja foi explicado , a demanda ótima,como a nova tabela de preço é a metade da máxima dos eixos, com 250 é possível comprar 50 unidades de X ou 25 unidades de Y. Demanda ótima = 25 de X e 12,5 de Y.
Demanda inicial >> Mas qual a demanda dos produtos ? vc saberia fazendo o seguinte : UmgX/UmgY = Px/Py , dai encontra uma relação entre X e Y, substituía na restrição orçamentaria e encontraria a demanda por X e Y. MAAAS, a questão facilitou bastante usando a função utilidade de cobb, elevada a 1/2, a demanda é a metade da quantidade máxima dos eixos, exatamente, a demanda ótima da primeira situação é 25 de X e 12,5 unidades de Y.
Efeito substituição = demanda com renda compensada. (x = 25, y=12,5 ) - Demanda inicial ( x=25,y=5)
ASSIM,
Efeito substituição em X. ESx = 25 - 25 = 0 . Efeito substituição em Y. ESy = 12,5 - 5 = 7,5.
Como a questão não pergunta se em X ou Y, e só há ES substituição em Y mesmo, então gab certo. Detalhe em relação ao sinal, positivo ou negativo, ensina o professor Varian, que o comportamento do efeito substituição é contrário ao comportamento do preço, ou seja, se o preço aumentou o efeito substituição é negativo. Perfeito o gabarito .
-
RESOLUÇÃO:
A equação de Slutsky nos diz que o Efeito Total = Efeito Substituição + Efeito Renda. Para encontrarmos o efeito substituição, precisamos olhar apenas para o efeito da variação dos preços.
Para conseguirmos calcular isso, precisamos, primeiro, ver qual era o equilíbrio do consumidor quando px = 2 e, depois, ver como o equilíbrio ficará quando px = 5. A partir daí, poderemos ver como se dará o efeito substituição. Para que consigamos isolar o efeito substituição, temos que supor que as quantidades consumidas não se alteram, mas a renda, sim.
Então, vamos ao cálculo da cesta originalmente escolhida – antes da mudança no preço!
A função de utilidade é a seguinte: . Repare que esta é um função Cobb-Douglas, pois segue o formato U = X.Y.
Numa função do tipo Cobb-Douglas, o consumidor demanda X assim:

Ou seja, no equilíbrio inicial, o consumidor consome 25 unidades do bem X e 5 do bem Y. Isso acontece quando a renda do consumidor é 100, px é 2 e py é 10. Bom, com isso em mente, podemos concluir que o consumidor gasta $50 com o bem x (25 unidades consumidas de x vezes o preço de x que é 2: 25.2 = 50). Além disso, o consumidor gasta os mesmos $50 com o bem Y: 5x10 = 50.
Mas a hipótese da questão é que px subiu de 2 para 5. Neste caso, teremos um novo equilíbrio e o consumidor mudará a quantidade consumida de x.
Como o py não mudou, podemos concluir que o consumidor demandará o mesmo de Y. Ou seja, o consumidor continuará gastando $50 para o bem Y.
No entanto, o bem x está mais caro. Se o consumidor quiser consumir as mesmas 25 unidades do bem x, ele terá que gastar mais (já que o preço de x aumentou). Ele irá gastar 25.5 = 125.
Portanto, se o consumidor, mesmo com o aumento de preço do bem x, quiser continuar consumindo 25 unidades do bem x e 5 do bem Y, a sua renda precisará ser de $175 (pois ele gastará $125 com X e $50 com Y).
Como o preço de Y era $10 e o consumidor demandava 5 unidades do bem, gastava $50 com Y.
Para continuar demandando 25 unidades de X, ao novo preço, precisaria de mais $125, além dos $50 gastos com Y. Isso totalizaria uma renda necessária de $175 para manutenção do poder aquisitivo.
Então, calculamos a nova quantidade ótima de X para o novo preço e a nova renda:
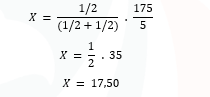
Note, então, que nesta nova situação, a quantidade demandada ótima de X é 17,5.
Antes, o consumidor consumia 25 unidades do bem X. No novo equilíbrio, ele consome 17,5 unidades. Se fizermos 17,5 – 25 (variação: final – inicial) , chegaremos a -7,5. Este – 7,5 significa que quando o bem x subiu de preço, o consumidor deixou de consumir 7,5 do bem x. .
Esse “deixou de consumir” é justamente o efeito substituição da equação de Slutsky.
Resposta: C
-
Fala pessoal! Tudo beleza com vocês? Professor Jetro Coutinho na área, para comentar esta questão sobre efeito substituição.
A equação de Slutsky nos diz que o Efeito Total = Efeito
Substituição + Efeito Renda. Para encontrarmos o efeito substituição,
precisamos olhar apenas para o efeito da variação dos preços.
Para conseguirmos calcular isso precisamos, primeiro, ver
qual era o equilíbrio do consumidor quando px = 2 e, depois, ver como o
equilíbrio ficará quando px = 5. A partir daí, poderemos ver como se dará o efeito
substituição. Para que consigamos isolar o efeito substituição, temos que supor
que as quantidades consumidas não se alteram, mas a renda, sim.
Então, vamos ao cálculo da cesta originalmente escolhida –
antes da mudança no preço!
A função de utilidade é a seguinte: u = 5x1/25y1/2. Repare
que esta é uma função Cobb-Douglas, pois segue o formato U = Xa.Yb.
Numa função do tipo Cobb-Douglas, o consumidor demanda X
assim:

E demanda Y de forma análoga:

Lembre que “a" e “b" são os expoentes de X e de Y,
respectivamente. No caso da equação utilidade desta questão, u = 5x1/25y1/2, tanto
“a" quanto “b" são iguais a ½.
Substituindo os valores dados pelo enunciado (a = ½, b = ½,
w = 100 e px = 2), temos:
X = 1/2/ (1/2 + 1/2)*100/2
X = 1/2/1*50
X = 50/2 = 25
Y = 1/2/ (1/2 + 1/2)*100/10
Y = 1/2/1*10
Y = 10/2 = 5
Ou seja, no equilíbrio inicial, o consumidor consome 25
unidades do bem X e 5 do bem Y. Isso acontece quando a renda do consumidor é
100, px é 2 e py é 10. Bom, com isso em mente, podemos concluir que o
consumidor gasta $50 com o bem x (25 unidades consumidas de x vezes o preço de
x que é 2: 25.2 = 50). Além disso, o consumidor gasta os mesmos $50 com o bem
Y: 5x10 = 50.
Mas a hipótese da questão é que px subiu de 2 para 5. Neste
caso, teremos um novo equilíbrio e o consumidor mudará a quantidade consumida
de x.
Como o py não mudou, podemos concluir que o consumidor
demandará o mesmo de Y. Ou seja, o consumidor continuará gastando $50 para o
bem Y.
No entanto, o bem x está mais caro. Se o consumidor quiser
consumir as mesmas 25 unidades do bem x, ele terá que gastar mais (já que o
preço de x aumentou). Ele irá gastar 25.5 = 125.
Portanto, se o consumidor, mesmo com o aumento de preço do
bem x, quiser continuar consumindo 25 unidades do bem x e 5 do bem Y, a sua
renda precisará ser de $175 (pois ele gastará $125 com X e $50 com Y).
Como o preço de Y era $10 e o consumidor demandava 5
unidades do bem, gastava $50 com Y.
Para continuar demandando 25 unidades de X, ao novo preço,
precisaria de mais $125, além dos $50 gastos com Y. Isso totalizaria uma renda necessária
de $175 para manutenção do poder aquisitivo.
Então, calculamos a nova quantidade ótima de X para o novo
preço e a nova renda:
X = 1/2/ (1/2 + 1/2)*175/5
X = 1/2/1*35
X = 35/2 = 17.5
Note, então, que nesta nova situação, a quantidade demandada
ótima de X é 17,5.
Antes, o consumidor consumia 25 unidades do bem X. No novo
equilíbrio, ele consome 17,5 unidades. Se fizermos 17,5 – 25 (variação: final –
inicial), chegaremos a -7,5. Este – 7,5 significa que quando o bem x subiu de
preço, o consumidor deixou de consumir 7,5 do bem x. .
Esse “deixou de consumir" é justamente o efeito substituição
da equação de Slutsky.
Gabarito do Professor: CERTO.