-
Encontramos diversas situações em Engenharia em que as peças estão solicitadas simultaneamente pela ação de momentos fletores e esforços normais. •
A esse tipo de solicitação denominamos flexão composta.
Note que a pergunta já indica uma das solicitações (flexão - momento fletor)
-
Gabarito: B
FLEXÃO COMPOSTA: ocorre o esforço de flexão composta quando a resultante das tensões normais pode ser decomposta em uma força normal e momentos fletores (ação de flexão).
-
Flexão composta: é caracterizada pela combinação do momento fletor e da força normal na seção transversal.
Flexão simples: é normalmente resultante da ação de carregamentos transversais que tendem a curvar o corpo.
-
Flexão Simples: Ação de uma cortante resultando em um momento fletor, curvatura. (N=0, Q≠0, M≠0)
Flexão Composta: Ação de uma força obliqua à superfície da estrutura, gerando uma componente normal e outra cortante, resultando em um momento fletor e uma força axial, curvatura+tração/compressão (N≠0, Q≠0, M≠0)
Flexão Pura: Ação apenas de momentos fletores puros na peça analisada, ou seja, a peça possui diagrama de normais e cortantes nulos, e de momentos fletores diferente de zero. (N=0, Q=0, M≠0)
-
Aí está um exemplo de flexão normal composta: Imagine uma viga de madeira servindo de suporte a um tablado em uma estrurura sobre um rio (uma ponte). Se o terreno comprimir essa viga ela estará sob flexão simples+compressão do terreno - força normal de compressão - resultando em uma flexão normal composta.
-
A flexão composta é a atuação simultânea do momento fletor e do esforço normal que resulta em tensões normais na peça.
A flexão composta divide-se em: flexão composta simples e flexão composta oblíqua.
Na flexão composta simples, há, além do esforço normal (N), a ocorrência de um momento fletor (M) na peça. Este é o caso clássico dos pilares de extremidade ou de borda (ver figura).
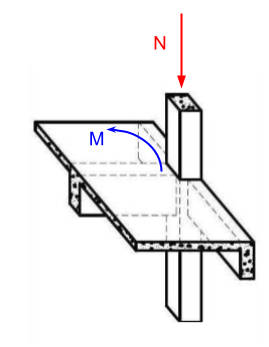
Na flexão composta oblíqua, há, além do esforço normal, a ocorrência de dois momentos fletores em duas direções na peça. Este é o caso clássico dos pilares de canto (ver figura).

Gabarito do Professor: Alternativa B.
-
Resumindo:
Flexão Pura : Momento Fletor
Flexão Simples: Momento Fletor + Cortante
Flexão Composta: Momento fletor + Força Normal