-
2 escolhidos de 30; só quem esteve em 2 dos paises A, B e C foram 6(A∩B);
então seria:
P=(6/30).(5/29)=1/29. Mas 1/29 é Maior que 1/30. O que torna a questão Errada.
Não entendeu? Procure por facebook.com/mathematik69 e saiba mais.
-
GABARITO - ERRADO
calculando a probabilidade – esses passageiros só podem ser os 6 que visitaram A e B – temos:
P = 6/30 X 5/29 = 1/29, que é maior que 1/30.
FONTE - ALFACON
-
OUTRA MANEIRA DE RESOLVER
6 PESSOAS QUE ESTIVERAM EM DOIS PAÍSES DO TOTAL DE 30 PESSOAS
6/30: 0,2 PESSOAS : 1/30
ENTÃO 2 PESSOAS SÃO 10/30.
GABARITO: ERRADO
-
PARA RESOLVER ESTA QUESTÃO TEMOS QUE CONTAR A QUANTIDADE DE PESSOAS QUE ESTIVERAM NOS PAÍSES A E B (6 PESSOAS) , A PARTIR DISSO A POSSIBILIDADE DE O 1° INDIVIDUO SELECIONADO SER DESSE GRUPO É 6/30 , (AO TIRARMOS O PRIMEIRO INDIVIDUO AGORA TEMOS 29 NO TOTAL) A PROBABILIDADE DE O 2° INDIVIDUO TAMBÉM SER DESSE GRUPO SERÁ DE 5/29.
FEITO ISSO MULTIPLICAMOS AS PROBABILIDADES:
6/30X5/29= 30/870--------- SIMPLIFICANDO FICA 1/29.
LOGO A PROBABILIDADE DE OS 2 INDIVIDUOS ESCOLHIDOS TEREM ESTADO EM 2 PAÍSES É DE 1/29 , LOGO MAIOR QUE 1/30.
-
Galera. Eu fiz de um jeito diferente que o resultado deu como sendo superior a 1/30, por isso gabarito errado e eu acabei acertando a questão. No entanto, o resultado da minha conta foi diferente. Alguém pode me ajudar a identificar em que parte exatamente do meu raciocínio eu errei? Segue:
Espaço amostral: 30 pessoas;
O que eu quero: 2 das 6 pessoas que estiveram em A e em B; Logo, C 6,2
6!/2!4! = 6.5/2 = 30/2 = 15 possibilidades
Então fica: o que eu quero / espaço amostral => 15/30
15/30 é maior que 1/30, logo, gabarito ERRADO.
Podem me ajudar? Matemática é meu calcanhar de Aquiles.
-
O final do exercício diz: "6 desses 25 passageiros estiveram em A e em B", ENTÃO 06 ESTIVERAM EM DOIS PAÍSES.
Vou selecionar 2 passageiros logo: passageiro e passageiro
6/30 e 5/29 6x5 =30 dividido por 30x29= 870 simplificando 30 por 870 dá resultado 1/29
GABARITO ERRADO
-
Galera, vcs tão deixando passar uma coisa.
São 30 no total, mas somente 25 passageiros foram examinados. Ou seja, não conseguimos saber o destino de 5 passageiros, que também podem ter ido para dois países.
Assim, não tem como afirmar que apenas 6 passageiros foram para dois países, pois não sabemos para onde foram esses 5 passageiros que não foram examinados.
Faz sentido??
-
Galera, vcs tão deixando passar uma coisa.
São 30 no total, mas somente 25 passageiros foram examinados. Ou seja, não conseguimos saber o destino de 5 passageiros, que também podem ter ido para dois países.
Assim, não tem como afirmar que apenas 6 passageiros foram para dois países, pois não sabemos para onde foram esses 5 passageiros que não foram examinados.
Faz sentido??
-
NÃOvaiREELEGER Ninguém ,
eu tinha notado isso também, mas analisando essa parte do enunciado "Constatou-se que exatamente 25 dos passageiros selecionados estiveram em A ou em B" ,ou seja não pode entrar mais ninguém nesses dois paises (25 exato), então podemos concluir que os 5 restantes devem ficar necessariamente somente em C. Portanto, somente 6 mesmo visitaram dois paises.
ERRADO.
-
NÃOvaiREELEGER Ninguém a questão não diz que somente 25 foram examinados. Foram examinados 30 e, desses 30, "exatamente 25 dos passageiros selecionados estiveram em A ou em B" e "nenhum desses 25 passageiros esteve em C".
Se nenhum desses 25 esteve em C, e são 30 no total, então os 5 restantes só podem ter ido para C.
Ainda, se nenhum dos 25 esteve em C, então não há intersecção entre C e os outros dois conjuntos.
-
países A;B;C
25 visitaram A ou B
6 vísitaram A e B (intersecção)
5 visitaram C e quem visitou este não visitou nenhum outro, logo somente quem (visitou A e B são as possibilidades de ter visitado mais de um país, já que em visitou C não visitou nenhum outro, e tem aqueles que só visitaram A ou somente B)
P=6/30.5/30=1/5.5/29=1/29 Se eu estiver errado peço que me corrijam. Foco Força e FÉ em DEUS.
-
Vamos descomplicar
Se 2 dos 30 passageiros selecionados forem escolhidos ao acaso, então a probabilidade de esses 2 passageiros terem estado em 2 desses países é inferior a 1/30.
Total de passageiro = 30
Passageiro selecionado = 2
P = 2/30
Resposta errada, 2/30 é superior a 1/30
-
Que confusão que o povo está fazendo...
-
A questão quer saber a probabilidade de 02 passageiros terem estado nos dois países. Então:
o quê eu quero? R.: 02 passageiros que estiveram nos dois países
quantos passageiros estiveram nos dois países? R.: 06
neste caso, fazemos a seguinte conta: Probabilidade= o quê eu quero
o quê eu tenho
Em outras palavras dividimos o quê eu quero, pelo o quê eu tenho, desta forma 2/6 = 1/3 um terço é maior que 1/30
-
6/30 x 5/29 - 1/29
-
Galera, muitos comentários errados. CUIDADO!
A probabilidade é calculada da seguinte forma: o que eu quero / o que tenho.
Pessoas nos dois países: 6
Total de pessoas: 30
Quantas eu quero: 2
Logo: 6/30 x 5/29 R: 1/29
-
A questão ja diz que: 6 desses 25 passageiros estiveram em A e em B.
Para escolher 2 dos 30 passageiros terem estado em 2 desses países, temos:
6/30 x 5/29 = (simplicando 5.6 = 30) = 1/29
1/29 é maior que 1/30(lembrem-se, nas frações quanto maior for o denomindador, menor será seu resultado)
Fonte: Profª Rosa Figueirôa
-
Questão explicada pelos colegas acima, o que pegou mesmo foi lembrar que 1/29 é maior que 1/30, essa foi a pegadinha da questão.
-
C (30,2) 30.29 / 2.1= 435
C (6,2) 6.5 / 2.1=15
15/435 = 1/29
-
6/30 x 5/29 = 1/29
1/29 é maior que 1/30
-
Vc chega direitinho em 1/29 e pra responder considera que é menor que 1/30 kkkkkkkkkkkkkkkkkkk cabeça morreu por hoje!
-
Comentários de França e Wagner foram esclarecedores, obrigada!
-
6/30 X 5/29 =
Simplificando tudo daria 1/29, que é MAIOR que 1/30
-
6/30 x 5/29 = 1/29
1/29 é maior que 1/30
Ex. Imagine uma caixa dividida em quatro partes 1/4 |+|
Agora imagine uma caixa divida ao meio 1/2 |--|
Quanto maior o n° de partes dividida menor será o meu pedaço ou seja 1/2 > 1/4
-
GABARITO - ERRADO
PARA RESOLVER ESTA QUESTÃO TEMOS QUE CONTAR A QUANTIDADE DE PESSOAS QUE ESTIVERAM NOS PAÍSES A E B (6 PESSOAS) , A PARTIR DISSO A POSSIBILIDADE DE O 1° INDIVIDUO SELECIONADO SER DESSE GRUPO É 6/30 , (AO TIRARMOS O PRIMEIRO INDIVIDUO AGORA TEMOS 29 NO TOTAL) A PROBABILIDADE DE O 2° INDIVIDUO TAMBÉM SER DESSE GRUPO SERÁ DE 5/29.
FEITO ISSO MULTIPLICAMOS AS PROBABILIDADES:
6/30X5/29= 30/870--------- SIMPLIFICANDO FICA 1/29.
LOGO A PROBABILIDADE DE OS 2 INDIVIDUOS ESCOLHIDOS TEREM ESTADO EM 2 PAÍSES É DE 1/29 , LOGO MAIOR QUE 1/30.
-
GABA: E
https://www.youtube.com/watch?v=kBW_JFsGI64&t=220s
Resolução 10:50 min
-
Meu Deus, o pessoal faz umas contas exageradas para encontrar a resposta, sendo que é uma questão de puro raciocínio.
-
Não precisa fazer conta nenhuma...
-
Como são dois passageiros escolhidos entre seis (este é o total dos que estiveram em dois países, A e B), ao retirar o primeiro de um total de trinta, sobrarão cinco passageiros para serem escolhidos novamente num total de vinte e nove.
-
Errado
Probabilidade = o que eu tenho dividido pelo que eu quero!
1/30 = 0,333
2/30 = 0,666 - fração maior.
-
Como posso concluir que os 5 passageiros estiveram somente no país C? Eles podem ter ido ao pais C e A ou aos países C e B, a questão não dá essa informação. Tem furo nessa questão.
-
Outra possibilidade:
Pegar a probabilidade de selecionarmos 2 passageiros que visitaram os países A e B (que são 6) sobre a probabilidade de selecionarmos 2 passageiros aleatoriamente do total (que é 30). Então é só aplicar a fórmula de combinação, pois a ordem não importa.
Fórmula: C6,2 / C30,2 ==> 15 / 435 ==> 1/29
Logo: 1/29 é maior que 1/30
Resposta: Errado
-
Questão Média 76 %
Gabarito Errado
Diagrama de Venn
ABC:
sóAB:
sóAC:
sóBC:
sóA:
sóB:
sóC:
1º Etapa: 25 dos passageiros selecionados estiveram em A ou em B, nenhum desses 25 passageiros esteve em C.
Vamos dividir o grupo de 30 em 2 grupos:
O grupo de 25 pessoas estiveram em A e/ou B
O grupo de 5 pessoas estiveram somente em C
Então:
O conjunto que estiveram só em C
sóC: 5
O conjunto que estiveram em todos os elementos
ABC: 0
O conjunto que estiveram em A e C
sóAC: 0
O conjunto que estiveram em B e C
sóBC: 0
2º Etapa: 6 desses 25 passageiros estiveram em A e em B.
sóAB: 6
Diagrama de Venn
ABC: 0
sóAB: 6
sóAC: 0
sóBC: 0
sóA: ?
sóB: ?
sóC: 5
3ª Etapa: A probabilidade de 1 passageiro estiver em 2 países:
6 (sóAB) + 0 (sóAC) + 0 (sóBC) = 6 de 30
6 de 30 = 1/5
4ª Etapa: A probabilidade de 2 passageiros estiverem em 2 países
1/5 * 1/5 = 1/25
1/25 não inferior a 1/30.
1/25 é superior a 1/30.
http://sketchtoy.com/68912110
Bendito seja o nome do SENHOR!
-
Comentário do RENATO HINGEL me parece o certo. Há comentários com resultados equivocados.
-
SEPARE EM GRUPOS
25 estiveram em A ou B (TOTAL), sendo o que eu quero é as pessoas que foram em 2 países (6 TOTAL)
P= 6/25 * 5/24 = 30/750 SIMPLIFICANDO POR 3 1/25.
Gab: Errado
-
SOMENTE 6 ESTIVERAM EM 2 PAÍSES, LOGO, TEM-SE ===> 6/30 A POSSIBILIDADE DE ESCOLHER UMA PESSOA QUE ESTEVE EM 2 PAÍSES, COMO ELE QUER DUAS ENTÃO TEMOS==> 6/30 CHANCES DE ESCOLHER AO ACASO NA PRIMEIRA ESCOLHA E 5/29 CHANCES NA SEGUNDA;
Como ele quer 2 pessoas que estiveram exclusivamente em 2 países, logo tem-se-->
(6/30)*(5/29)= 30/870, simplificando 30/870 tem-se 10/290, simplificando novamente tem-se 1/29.
COMO EU SEI QUE É MAIS VANTAJOSO DIVIDIR UM LITRO DE WISKY IGUALMENTE COM 29 PESSOAS DO QUE COM 30, POIS SOBRARÁ MAIS PARA MIM ENTÃO POSSO DIZER QUE 1/29>1/30.
-
Somente 6 passageiros estiveram em A e em B.
Então a probabilidade é calculada 1/6 * 1/5
O resultado será exatamente 1/30.
Logo, a questão está errada, pois não é inferior, nem superior, mas igual a 1/30.
-
-
Lembro-me de errar no dia prova por nervosismo, porque atenção é o diferencial nestas questões.
Devemos investigar quem esteve em dois países, percebemos que são 6 em um espaço amostral de 30 passageiros.
6/30 x 5/29 = 1/29
1/29 > 1/30
GABARITO: ERRADO
-
Informação boba, mas que talvez seja relevante para quem está começando: para se descobrir qual fração é maior, faça a divisão.
Exemplo
Na questão, é dada a fração 1/30. O resultado é 1/29. Qual fração é maior? Dívida 1 por 30 e depois 1 por 29.
1÷30 = 0,033
1÷29 = 0,034
Logo, 1/29 é maior do que 1/30.
-
só olhando a questao já respondi errado pelo seguinte: a soluçao está na pergunta 2 de 30, nunca pode ser inferior que 1/30 . proxima
-
Simplificar cortando o 6, 5 e o 30 pois 6*5=30 e sobra a fração 1/29 - logo 1/29 é maior que 1/30
-
GAB ERRADO
A E B = 6
6/30 SIMPLIFICANDO = 1/5 É SUPERIOR A 1/30. Quem divide menos fica com mais. Quem divide mais fica com menos.
-
Veja que temos 25 passageiros que estiveram APENAS em A ou B, de modo que os outros 5 passageiros estiveram APENAS em C. Veja ainda que 6 passageiros estiveram A e B. Somente estes 6 de um total de 30 pessoas estiveram em dois países, como quer o enunciado deste item.
O número de casos FAVORÁVEIS pode ser obtido combinando-se as 6 pessoas que estiveram em dois países em grupos de 2 pessoas:
FAVORÁVEIS = C (6,2) = 6x5 / (2x1) = 15 casos
O número TOTAL de casos é obtido combinando-se todas as 30 pessoas disponíveis em grupos de 2:
TOTAL = C(30,2) = 30x29 / (2x1) = 435
A probabilidade buscada é, portanto:
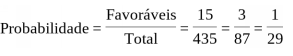
Este número é SUPERIOR a 1/30, visto que o seu denominador é menor. Item ERRADO.
Outra forma de resolução:
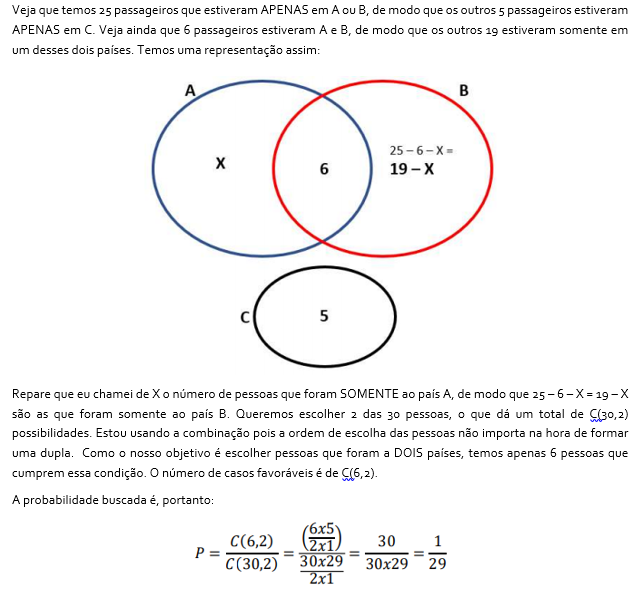
Este número é SUPERIOR a 1/30, visto que o seu denominador é menor. Item ERRADO
-
Simples, vamos lá:
A questão aborda sobre a intercessão entre A e B, sendo assim, vamos usa-la como pedido
1 - Temos um total de 30 pessoas e 6 foram em 2 países ( A e B), ou seja, 6/30 foram em 2 países.
2 - Se escolhermos 2 pessoas QUE FORAM NOS 2 PAÍSES faremos a seguinte escolha 6/30 e 5/29 (como na primeira eu ja escolhi, na segunda eu diminuo 1 de cada)
3- Multiplique 6x5 e 30x29 chegando ao total de 30/870.
4 - 30/870 dividindo tudo por 10 dá 3/87 e dividindo NOVAMENTE tudo por 3 chegamos a resposta de 1/29 (QUE É MAIOR QUE 1/30), nesse caso, no passo numero 4, usamos o método da SIMPLIFICAÇÃO PARA CHEGARMOS AO RESULTADO.
-
"2 passageiros terem estado em dois DESSES países" acaba prejudicando a questão. Porque pelo que eu tô vendo a maioria de vocês estão interpretando a questão como se ao acaso forem escolhidos duas pessoas que ambas visitaram A e B. O que pra mim é um entendimento errado! Veja se for pego a dupla (A,C) garantiu que esteve em dois países, assim como a dupla (B,C). Vocês estão fazendo as contas somente com a dupla (A e B, A e B) o que está errado! Por coincidência o gabarito da questão dá errado.
Tomem cuidado, são dois escolhidos ao acaso.
E outra, na primeira tentativa já matava a questão -> 6/30=1/5 que é superior a 1/30
Fazer (6/30)*(5/30)=1/29 quer dizer que: "AMBOS os passageiros estiveram em dois desses países"
-
A questão afirma que dos 25 passageiros que estiveram em A ou B, 6 desses estiveram em ambos, logo, entre os 30, há 6 que estiveram em 2 países.
6/30 x 5/29 < 1/30? (essa é a pergunta)
Simplificando essas frações, chega-se a:
1/29 < 1/30
Portanto, gabarito errado.
-
A grande sacada dessa questão não é só achar o 1/29, mas sim ter a percepção e clareza que que 1/29 é maior do que 1/30 (quem divide menos é maior).
1/29 = 0,0344827586206897 (MAIOR)
1/30 = 0,0333333333333333
-
vá direto ao Professor Ivan Chagas
-
Teoria da casa dos pombos!!!!!!!!!!!!
-
6 pessoas, dentre as 30 estiveram em 2 países.
Então pra pegar 1 passageiro que esteve nos dois a probabilidade é 6/30.
Pra pegar o segundo passageiro teremos 5, dentre os 29 (porque já escolhemos 1). 5/29
6/30 X 5 /29 = 1/29
1/29 > 1/30
GAB: Errado.
-
MERMÃO, FIZ O SEGUINTE:
QUANTOS TENHO?
30
QUANTOS FORAM PARA DOIS PAÍSES?
6
RASGUEI LOGO O VERBO E PIPOQUEI O CALCULO DA PROBABILIDADE:
PROBABILIDADE: O QUE EU QUERO 6
________________ = ___
TUDO QUE TENHO 30
6/30 SIMPLIFICANDO POR 6 FICA: 1/5
1/5 É MENOR OU MAIOR QUE 1/30???????
1/5= 0,2
1/30 = 0,03
0,2 < 0,03?????
NÃO É MENOOOOOR, VELHO!
GAB.: ERRADO.
-
ainda acredito que a resposta seja (6/25)*(5/24)= (1/20)
pois, as 5 pessoas do grupo C nunca estiveram em 2 países. Logo, nuca poderão ser contabilizadas...
desculpem os erros de português...
-
Das explicações nenhuma bateu com meu raciocínio, mas acertei a questao então vou explicar o que fiz e que foi bem simples. Talvez ajude.
O gabarito é Errado porque:
São dois passageiros ao acaso dos 30, sendo que estiveram em dois países. Só estiveram em dois países os 25 (em A e B)
Logo, a probabilidade é de 25/30 (pois é o numero de favoraveis sobre o numero de elementos), simplificando dá 5/6.
Fazendo uma conta rapida, 1/30=0,0333... e 5/6=0,8333...
Assim sendo superior a 1/30.
(Não sei se é o raciocínio correto, mas funcionou para mim)
-
vixe. fiz diferente
-
Nas questões CESPE precisamos interpretar o texto também:
- enunciado:
"30 passageiros" (total de elementos)
"6 desses 25 passageiros estiveram em A e em B", ou seja, 6 passageiros estirem em 2 países (elementos favoráveis)
- pergunta:
"Se 2 dos 30 passageiros selecionados forem escolhidos ao acaso", significa que vamos calcular 2 probabilidades (1ª pessoa x 2ª pessoa)
Logo,
P (F) = 6
P (T) = 30
6/30 (1ª pessoa) x 5/29 (2ª pessoa) = 1/29 (faça por simplificação)
Para não precisar fazer o calculo 1/29, imagine que irá dividir 1 real para 29 pessoas.
Faça o mesmo com 1/30, imagine que irá dividir 1 real para 30 pessoas.
Ora, com o número de pessoas menor você consegue distribuir um valor maior.
Assim,
1/29 (3,4% ou 0,034) é maior que 1/30 (3,3% ou 0,033).
-
PREMONIÇÃO DO CORONA VÍRUS
-
30 passageiros
25 estiveram em a ou b
6 estiveram em a e b
Dentro desses 30 qual a probabilidade de achar 2 que estiveram ema e b sabendo que apenas 6 estiveram lá
A resposta é 6/30 = 5
Achando o número 5 deduzimos que já temos1 passageiro agora falta mais um
Assim temosà 5 /29 o 29 épor conta que devemos levar em conta que 1 passageiro já foi encontrado
Então simplificamos à 6/30 e 5/29 à 1/29 ( se 6x5= 30, então cortamos 6, 5 e o 30 , sobrando 1/29)
1/29 < 1/ 30
-
Pessoal,
são 2 pessoas ao acaso dos países (A e B) = interseção (6);
-a questão afirma que é inferior (<) a 1/30. Vamos analisar:
—-probalidade=o que ele quer/ total
—-probabilidade = 6/30 < 1/30 (multiplica cruzado).
6x30= 180
1x30 = 30
180<30 ?? 180 menor que 30??
Errado
-
Probabilidade do Evento (E) = C 6,2 = 15
Espaço Amostral (A) = C 30,2= 435
15/435 = 0,034 = 3,4%
1/30 = 0,033 = 3,3%
3,4% > 3,3%
Gabarito errado.
Mais alguém ai levou esse raciocínio?
-
1) A ordem não importa! Logo, utiliza-se Combinação (Cn,p)
2) O enunciado pede a INTERSECÇÃO (/\) = 6, a qual se dará também em uma Combinação (Cn,p).
= C 6,2 / C 32,2
= 15/435
= 1/29 > 1/30
-
Meu raciocinio;
Total de possibilidade = C30,2 = 435
Possibilidades do que quero: C6,2= 15
435 / 15 = 29 "partes"
ou seja, o que quero equivale a 1/29 (uma das 29 partes) que obiviamente é maior que 1/30.
-
E
Quantos passageiros estiveram nos 2 países? -> 6
Desse modo: 6/30*5/29 = 30/30*29 -> corta os 30 = 1/29>1/30
-
Quero 1° E 2°
6/30 E 5/29
6/30 x 5/29
simplifica o 5 com o 30
6/6 x 1/29
1 x 1/29 = 1/29
1/29 > 1/30
-
6/30 * 5/29 = 30/870 = 3/87 (corta os zeros) = 1/29 (simplificado)
6 -> quantidade de passageiros que estiveram em dois países
30 -> quantidade total
5-> diminui um por dedução de quem o outro passageiro já foi escolhido
30-> diminui um por dedução de quem o outro passageiro já foi escolhido
Obs: Cada dia acredito que questões como essa são as que dão a aprovação. Resista!
-
1º- Espaço Amostral = 30. Pessoas que estiveram em A e B=6
2º- Primeira escolha: 6/30
3º- Segunda escolha: 5/29 (diminui um no numerador e um no denominador porque um já foi escolido na etapa anterior)
4º- Multiplicação da 1ª escolha pela 2ª: 6/30 x 5/29 = 30/870
5º- Simplificando por 30: 1/29
6º- CONCLUSÃO: Assertiva errada, pois 1/29 é maior (>) que 1/30. Basta pensar que, se dividir uma pizza em 29 fatias, cada fatia será maior que se dividisse a mesma pizza por 30.
Fiz assim. Se estiver errado, mandem mensagem.
-
C 6,2 / C 30,2
Combinação do resultado pretendido dividido pela combinação das possibilidades totais, ou seja de 2 passageiros visitando qualquer país.
-
Questão fácil e eu não soube fazer....
É luta
-
6/30 x 5/29 = (simplicando 5.6 = 30) = 1/29
-
Eu sou uma negação na matemática. Affff
-
6 passageiros visitaram + de 1 pais, 6/30
a questão pede 2 passageiros
1° pass ---- 6/30
2° pass ---- 5/29
probabilidade de 2 passageiros --- 6/30 . 5/29 (pois já pegou 1 passageiro e sobrou 29 pessoas) = 30/ 30 . 29 = 1/29
logo,
1/29 > 1/30
Gab = E
-
o cáuculo em si, não é complicado. o problema está em desenrolar a questão e saber a "formúla mágica" que deverá ser usada
-
DE 30 PASSAGEIROS QUERO 2: C30,2: 435
AGORA, QUERO DOIS PASSAGEIROS QUE TIVERAM EM DOIS DESSES PAÍSES.
Questão mesmo diz que 6 estiveram em A E B, LOGO QUERO 2 DOS 6: C 6,2: 15
R 15/435= 1/29 = 0,34
1/30= 0,33
R: 1/29 E MAIOR QUE 1/30.
-
Engraçado que todas os comentários são com a mesma resposta, depois que o vídeo do professor saiu todo mundo soube explicar rsrs
-
Fiz dessas 2 formas
1/30 + 1/29 = 2/59 simplifica por 2: 1/29
ou ( pra ter certeza )
1/30.100 = 100/30 = 0,33%
1/29.100 = 100/29 = 0,34%
-
TOTAL DE POSSIBILIDADES: C30,2 = 435 ---> 435
INTERSECÇÃO ENTRE OS 2 PAÍSES = C6,2 ----> 15
= 15/435
= 1/29
-
Pessoal no link abaixo temos a resolução em vídeo dessa questão .
Em nosso canal do YouTube JCMAulas, temos a resolução de mais questões e em nosso instagram @jcmaulas temos mais de 800 questões resolvidas e comentadas.
https://youtu.be/FCB0MqtdiH8
-
Eu fiz as tentativas na mão mesmo, como eram dois:
Tirar os 6 dentre os 30:
Primeira tentativa x segunda tentativa
6/30 x 5/29 = 30/870
O que só de não ser 30/900 que seria o mesmo que 1/30 já se percebia ser maior
Mas fazendo os cálculos:
30/870= 0,034
1/30=0,033
-
Vendo a galera resolver e tals, minha dúvida é:
eu poderia pensar dessa forma: montando o diagrama a gente percebe que 6 pessoas estiveram nos dois países, logo , 1/6 das pessoas estiveram nos dois países, 1/6 > 1/30, logo gabarito errado.????
-
Finalmente uma questão de estatística comentada.
-
ERRADO
-
ERRADO
-
A maioria das questões de probabilidade, você pode resolver com uma única fórmula: P = Favorável / Total
No total tem-se 30 pessoas das quais quer se escolher 2. Como a ordem não importa, temos um caso de combinação.
Total = C(30,2) = 30*29 / 2*1 = 15*29.
Para os casos favoráveis queremos escolher 2 pessoas que estiveram em dois países. Neste caso, 6 pessoas estiveram em dois países. Então, das 6, queremos escolher duas. Mais uma vez, a ordem não importa e fazemos uma combinação.
Favorável = C(6,2) = 6*5 / 2*1 = 15.
Portanto, ficamos assim: P = favorável / total => P = 15 / 15*29
P = 1/29.
comparando 1/29 e 1/30, nota-se que os numeradores são iguais e que os denominadores são diferentes. Em fração o menor denominador equivale ao maior resultado. Portanto, 1/29 > 1/30.
Resposta: ERRADO
-
ERRADO.
1/29 é maior do 1/30
-
Tenho que descordar da esmagadora maioria dos colegas e professores que resolveram a questão usando combinação.
Me corrijam, por favor, se eu estiver errado.
A questão pede PELO MENOS 1 pessoa que esteve em C.
A questão não pede que seja escolhida no MÁXIMO 1 pessoa de C.
Logo é possível que sejam escolhidas duas ou apenas 1 pessoa que esteve em C.
Se apenas 5 pessoas estiveram em C, o cálculo correto seria 5x29=140.
Passo 1. É preciso entender que 1 pessoa dentre 5 podem ser escolhidas inicialmente.
Passo 2. Depois multiplicaremos por todo o resto que sobrar, já que pessoas que estiveram em A, B ou C poderiam ter sido escolhidas.
Obs.: Considerando a primeira pessoa escolhida no passo 1 ela deve ser subtraída do passo 2, por isso é 5x29 e não 5x30.
Não sei se fui claro.
-
pessoal fiz da seguinte maneira:
sabe-se que dentre 25 (que não estiveram em C), 6 estiveram em A e B.
Logo, 5 estiveram somente em C. Pois o universo é 30 Passageiros
então a probabilidade de escolher 2 passageiros que estiveram em dois países é 6/30, que é igual a 1/5.
Tornando a questão errada.
está correto meu raciocínio?
-
6/30 x 6/30 = 1,2/30
-
Eu fiz por combinação: C6,2 (o que eu quero, que são as 6 pessoas que estiveram em A e B)/C30,2 (total de casos)= 1/29.
-
Se vc enxerga que apenas 6 dos 30 estiveram em A e em B, sendo esses os únicos a estarem em 2 países, e a questão quer a probabilidade de 2 passageiros terem estado em 2 dos 3 países, fica fácil julgar o item como errado.
Ela dá 1/30 e diz que a probabilidade do que foi pedido é inferior a essa.
"Se vc enxerga que apenas 6 dos 30 estiveram...": 6/30 (já daria pra julgar como errada).
Temos 6/30 x 5/29 (tirei um e tirei mais um). = 1/29
-
PESSOAL ATENÇÃO!!! 1/29 É MENOR QUE 1/30. NAO MARQUEM NO DESESPERO. FIZ A CONTA CERTA ACHEI 1/29 E NA EUFORIA MARQUEI CERTO.
-
180 > 30 Então = Errado
-
ERRADO
-
Olá pessoal,
Vejam o vídeo com a resolução dessa questão no link abaixo
https://youtu.be/wI6hpHxX9PU
Professor Ivan Chagas
www.youtube.com/professorivanchagas
-
Gab: errado
6 estiveram em dois países --> 6/30
retirei o primeiro --> retirando o segundo -->5/29
multiplicando 6/30 x 5/29 = 1/29
Obs: quanto maior o denominador ---> maior o numero
1/29 é maior que 1/30
-
fazer a conta certinho, chegar em1/29, e marcar que é inferior a 1/30. Esse sou eu :/
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/WrOn94oAJSA
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D
-
Resolvo essa questão aqui nesse vídeo
https://youtu.be/WrOn94oAJSA
Ou procure por "Professor em Casa - Felipe Cardoso" no YouTube =D
-
Resolução:
Ao total temos 30 passageiros.
O texto acima da questão afirma que apenas 6 passageiros estiveram em 2 países, os quais eram A e B, portanto, já temos nosso grupo de onde selecionaremos 2 pessoas.
6 5
P= ------ x -------
30 29
Basta simplificar o 30 com o 5 e depois o 6 com o 6, observe:
6 5 6 1
P= ------ x ------- = ------ x ---------- = 1/29 > 1/30
30 29 6 29
-
ERRADO
Total = 30 passageiros
Passageiros que estiveram em dois países = 6
6/30 x 5/29 = 30/870 = 1/29
1/29 > 1/30
-
Uma dúvida: não era simplesmente considerar que 2/30 > 1/30, portanto alternativa errada?
-
Simples:
6/30 x 5/29 = 6/6 x 1/29 = 1/1 x 1/29
R: 1/29
-
Talvez um dia, quem sabe, eu consiga entender RLM e Contabilidade.
-
(Obs) nessa fração, o numero que divide mais é inferior ao que divide menos.
6/30 de A 5/29 de B 5.6=30, 30 corta com 30. Então sobra 29.
-
NÃO COMPLICA, SIMPLIFICA:
APENAS 6 ESTIVERAM EM 2 PAÍSES...
SENDO ASSIM:
6/30 x 5/29 = (só simplificar) = 1/29
"dividir 1 em 30 partes fica menor do que dividir em 29 partes"
-
Eu fiz 2/25 < 1/30, porque quem esteve em dois países foram 25 pessoas, a probabilidade de sortear dois desses seria 2 (o que eu quero) sobre 25 (o total), ai coloquei essa fração menor que 1/30 e fiz o cálculo, por isso item errado.
-
COMENTÁRIOS TODOS TROCADOS !!!
-
Gab: Errado
Procure sempre lembrar dessa fórmula:
Resultados favoráveis / Resultados Possíveis
A e B = 6 pessoas
Total = 30
6/30 x 5/29 = 30/870 (como eu escolhi um passageiro, tirei ele dos totais, ficando 5/29)
Simplificando (divide em cima e em baixo por 30): 1/29
Logo, quem divide menos, fica com mais. Então 1/29 é superior a 1/30.
-
Também é possível fazer por combinação já que a ordem não importa. C(6,2) / C(30,2) termine o cálculo e chegará aos resultado.
-
C(6,2)/C(30,2)= 15/435=1/29, logo 1/29>1/30
ASSERTIVA: ERRADA
-
Errado
P(x) = (6/30/) * (5/29) = 1/29 >1/30
-
A questão diz que: 6 desses 25 passageiros estiveram em A e em B.
Com isso, o numero de grupos formados por 2 pessoas entre essas 6 é: 6! / 2! 4! = 15
O número total de grupos que podem ser formados com 2 pessoas é: 30! / 2! 28! = 435
Com isso a probabilidade é 15/435 = 1/29 que é superior a 1/30.
GABARITO ERRADO
-
6/30 * 5*29
simplifica
1/5 * 5*29
cancela 5 com 5
RESTANDO 1/29, LOGO → GABARITO ERRADO
#BORA VENCER
-
QUESTÃO MUITO BOA
Total → 30 pessoas
25 estiveram em A ou B
desses 25, nenhum deles foi em C
então, todos esses 25 foram em no máximo dois países
6 desses 25 foram em A e B, logo os 19 restantes somam aqueles que foram apenas em A e apenas em B
ou seja, 19 foram em apenas um país
6 foram apenas em A e B, já que desses 25 (6 que foram em A e B + 19 que foram parte em apenas A e outra parte em apenas B) nenhum deles foi em C
A questão diz que EXATAMENTE 25 foram em A ou em B, isto é, a quantidade exata de pessoas que foram nos países A ou B foram 25, os 5 restantes, portanto, não foram nem em A, nem em B. Repito, a questão deixa claro que dos 30, os que foram em A ou B foram apenas 25, o restante, portanto, só pode ter ido em C, somente em C.
então fica assim:
5 foram apenas em C
6 foram em A e B → foram em 2 países
19 visitaram apenas um país A ou B
Agora fica muito mais fácil descobrir a probabilidade de escolhendo duas pessoas, ao acaso, as duas terem visitado dois países
Casos favoráveis → 6 (são aqueles que visitaram dois países)
Casos possíveis → 30
6/30 x 5/29 = 1/29
-
Pessoas que estiveram A e B= 6;
Total = 30;
6/30*5/29=> 6*5/30*29=>30/30*29=>1/29
Corta 30 em cima e 30 embaixo.
-
probabilidade você vai dividir
o que ele quer/ tudo que pode sair
1° passageiro 6/30
2° passageiro 5/29 (note que no 2° já foi encontrado o 1° por isso 5/29)
6 .........5
___ x ___ = 30/870 simplificando = 1/29
30 ......29
logo 1/29 é maior que 1/30.
-
Resposta: 6/30 x 5/29 = 1/29
Conclusão: a probabilidade será no mínimo igual a 1/29
Veja que por essa resolução não estamos considerando os 5 passageiros restantes, mas isso pouco importa. Se considerarmos os 5 restantes, a probabilidade só irá aumentar, e continuará sendo maior que 1/30.
Dito de outra forma: a probabilidade de 1/29 é uma probabilidade mínima. Se considerarmos os 5 passageiros restantes, essa probabilidade será ainda maior.
Gabarito: Errado
-
Por que eu não posso simplesmente dividir o número de passageiros que estiveram nos dois paises pelo total de passageiros?
-
Quantos passageiros foram para o país A e B? 6 passageiros.
Se 2 dos 30 (total) forem escolhidos, então:
Probabilidade = QUERO / TENHO, assim:
6 / 30 x 5 / 29 = 30 / 870 (corta os zeros) = 3/87 (simplifica por 3) = 1/29.
Como saber se 1 / 29 é inferior a 1/30? Multiplicando cruzado os números de baixo.
30 x 1 = 30
29 x 1 = 29
Qual é o maior? 1/29, que deu o número 30. Assim, 1/29 é maior que 1/30, não é inferior.