-
E = 1,65 = Vv/Vs -> Vv = 1,65Vs
h = 0,75 = ma/ms -> ma = 0,75ms
ms/Vs = 26,5
Ynat = mt/vt -> ma + ms /Vv + Vs -> 0,75ms +ms /1,65Vs + Vs -> 1,75ms/2,65Vs = 1,75*26,5/2,65 = 17,5kN/m³
-
Outro modo de resolver seria:
γs = γd . (1 + e)
γd = γs / (1 + e) = 26,5 / (1 + 1,65) = 10 KN/m³
γn = γd . (1 + w) = 10 . (1 + 0,75) = 17,5 KN/m³
____________________________________________
γs - peso específico dos sólidos
γd - peso específico aparente seco
γn - peso específico natural
e - índice de vazios
w - teor de umidade
-
Para responder essa pergunta
devemos colocar em prática nosso conhecimento sobre Mecânica dos Solos.
O solo consiste na
camada superficial da Terra, oriundo dos processos de intemperismo e
decomposição das rochas. O mesmo é formado por uma fase sólida, composta de
matéria orgânica e inorgânica; uma fase líquida, associada à água ou outra
solução presente no solo; e uma fase gasosa, correspondente aos gases no solo.
No problema em questão, o
peso específico natural pode ser determinado empregando as seguintes equações:

Visto isso, isolando o peso
específico aparente seco do solo na primeira expressão e substituindo os dados
fornecidos pelo enunciado do problema, resulta que:
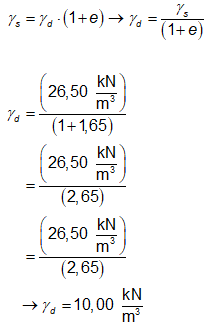
Por fim, substituindo o
valor de γd encontrado e o valor de w fornecido pelo enunciado na segunda
expressão citada, o valor do peso específico natural do solo fica determinado:
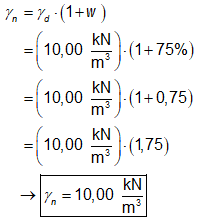
Logo, o peso específico
natural do horizonte de solo do problema é de 17,5 kN/m³ e, portanto, a
alternativa C está correta.
Gabarito do professor: Letra
C.
-
Yn = Ys x (h+1)/(e+1)
Yn = 26,5 x (0,75+1)/(1,65+1)
Yn = 17,5 kN/m3
Onde:
Yn = Peso Especifico Natural
Ys = Peso Especifico Sólido
h = Umidade (%)
e = Indice de vazios (Grandeza Adimensional)
Simples Assim, uma aplicação trivial de fórmula:
A impressão que dá é que os alunos de Engenharia tem o prazer de repassar as resoluções de uma forma dificil para aparentar uma suposta superioridade, triste isso, sejam mais objetivos nas resoluções de exercicios