-
Gabarito: ERRADO
Raio hidráulico (R) - relação entre a área molhada e perímetro molhado.
R = A / P = b * h / b + 2 * h
-
Não entendi o gabarito. Alguém pode postar a resolução, obrigado!
-
Para uma mesma largura de base, se aumentar a profundidade, o raio hidráulico aumenta.
-
Como a largura não foi especificada se era de fundo ou superfície, em razão da inclinação do talude e da profundidade, considerei 3m como a largura da base.
Para profundidade 4m:
Am1=((11+3)/2)*4 = 28m²
Pm1=4*√2 + 4*√2 + 3 = 14,31m
Rh1=28/14,31 = 1,95
Para profundidade 3m:
Am2=((9+3)/2)*3 = 18m²
Pm2=3*√2 + 3*√2 + 3 = 11,48m
Rh2=18/11,48 = 1,57
Rh1>Rh2 , portanto Gabarito: ERRADO
Pelo conceito teórico → O raio hidráulico é uma medida de eficiência hidráulica. Quando maior a quantidade de água escoando com uma menor superfície de contato, maior a eficiência e maior o raio hidráulico.
Espero ter ajudado.
-
Para responder essa
pergunta devemos colocar em prática nosso conhecimento sobre Hidráulica,
especificamente sobre o conceito de raio hidráulico.
No dimensionamento de
condutos livres, um parâmetro de grande importância para o pré-dimensionamento
das seções é o raio hidráulico (Rh). O mesmo é, por definição, o quociente
entre a área da seção transversal molhada (Am) e o perímetro molhado (Pm).
Matematicamente, podemos escrever que:
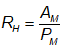
Para
todos os casos, devemos relembrar que a área de um trapézio consiste na
média entre a base menor e a base maior multiplicada pela altura; e que o perímetro
inclinado em taludes laterais com inclinação 1:1 é de √2 para cada metro de
altura. Visto isso, Para o canal com profundidade de 4 m, tem-se que:

Por sua
vez, para o canal com altura de 3 m:

Logo, o
raio hidráulico com profundidade de 4 m é superior ao raio hidráulico
para a profundidade de 3 m. Portanto, a assertiva do enunciado está
errada.
Gabarito
do professor: ERRADO.
-
B = base maior
b = base menor = B-2*(h) --> talude 1:1
h = profundidade
l = largura = 3
Como b=3 --> B=b+2h --> B=3+2h
Rh = A/P
A = (B+b)*h/2 --> A = (3+2h+3)*h/2 --> A = 3h+h²
P = B + 2*talude
P = B + 2*h*raiz(2)
Rh = (3h+h²)/(B+2*h*raiz(2)) --> (3h+h²)/(3+2h+2*h*raiz(2))
P/ h=3 --> (3*3+3²)/(3+2*3+6raiz(2))
18/(9+6raiz(2)) --> 6/(3+2raiz(2)) = 1,029
P/ h=4 --> (3*4+4²)/(3+2*4+8raiz(2))
28/(11+8raiz(2)) = 1,255
-
Altura de 4m.
Talude com proporção de 1:1 = Altura de 4m, largura de 4m <TALUDE, não do canal>
Vai ficar um trapézio de:
- 11m <base maior> 4m + 3m + 4m = 11m
- 3m <base menor>
- um talude de aproximadamente 5,6m
Raio Hidráulico = Área molhada / Perímetro Molhado.
Área Molhada = [(B + b ) / 2 ] x h = [(11 + 3 ) / 2 ] x 4 = 28m².
Perímetro Molhado = 5,6m + 3m + 5,6m = 14,2m <5,6m é o talude>
Rh = 28 / 14,2 = 1,97m.
Altura de 3m.
Talude com proporção de 1:1 = Altura de 3m, largura de 3m <TALUDE, não do canal>
Vai ficar um trapézio de:
- 9m <base maior>
- 3m <base menor>
- um talude de aproximadamente 4,24m
Raio Hidráulico = Área molhada / Perímetro Molhado.
Área Molhada = [(B + b ) / 2 ] x h = [(9 + 3 ) / 2 ] x 3 = 18m².
Perímetro Molhado = 4,24m + 3m + 4,24m = 11,48m <4,24m é o talude>
Rh = 18 / 11,48 = 1,56m.
1,97 > 1,56 Gabarito ERRADO