-
40=Lmm/R
40=200/R
R=200/40
R=5
-
Devido à esbeltez reduzida, a norma ABNT NBR 7190:1997 considera que o dimensionamento de peças curtas (λ 40) não sofre a interferência de tensões adicionais provocadas por eventual flexão do elemento estrutural comprimido.Para esta situação, o raio de giração mínimo (i) em cm é dado para o maior valor de índice de esbeltez possível (λ = 40), sendo o comprimento teórico de referência (Lo) fornecido pela questão de 200 cm, logo:
λ = Lo (cm) / i (cm)
i = Lo / λ
i = 200 (cm) / 40
i = 5 cm
-
Solução: https://youtu.be/AmTfNk1An-U
-
Para que não sofra efeitos de flexão, a peça deve ser curta, com índice de esbeltez máx = 40.
λ = L/raio de giração
Raio de giração = 200/40
Raio de giração = 5 cm
Limites:
λ < 40 (peça curta)
40 < λ ≤ 80 (semiesbelta)
80 < λ ≤ 140 (esbelta)
-
A questão exigiu conhecimento a respeito do raio de giração mínimo
para efeito de dimensionamento de pilares de madeira.
Matematicamente, o índice de esbeltez é calculado pela seguinte
equação:"
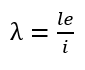
Onde:
λ = índice de esbeltez;
le = comprimento equivalente;
i - raio de giração.
De acordo com o índice de esbeltez, os pilares podem ser classificados
em:
λ < 40; pilares curtos;
40< λ < 90: medianamente esbelto;
90< λ < 140: esbelto;
140< λ< 200: muito esbelto.
Assim, para calcularmos o raio mínimo (i) da peça
de madeira é necessário conhecer o índice de esbeltez para essa situação de
projeto, já que o comprimento equivalente foi fornecido.
Esse valor é encontrado no seguinte trecho da NBR
7190/1997 - Projeto de estruturas de madeira:
“7.5.3 Compressão de peças curtas
Para as peças curtas, definidas pelo índice de
esbeltez igual a 40, que na situação de projeto são admitidas como solicitadas
apenas à compressão simples, dispensa-se a consideração de eventuais efeitos de
flexão. “
Logo, substituindo os dados na expressão do índice
de esbeltez, tem-se:
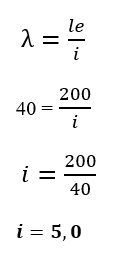
Resposta do professor: Letra C.
FONTE:
ASSOCIAÇÃO
BRASILEIRA DE NORMAS TÉCNICAS NBR 7190 - Projeto de
estruturas de madeira. Rio de Janeiro, 1997.
-
Uma crítica a questão: faltou a informação sobre as condições de contorno.
A própria norma admite que em condições de contorno com engaste em uma extremidade e liberdade de outra, admite-se Lo = 2 x L.
Caso a peça seja indeslocável em ambas extremidades considera-se Lo = L.