Tv = tensão vertical
T'v= tensão vertical efetiva
u=poropressão
Th= tensão horizontal total
T'h= tensão horizontal efetiva
k0 = coef. de empuxo no repouso (só usado para tensões efetivas)
1) Tv= somatório do peso específico x profundidade = 19x6= 114kN/m²
2) u= peso da água x profundidade da água = 10x4 = 40kN/m²
3) T'v= Tv-u = 114-40= 74 kN/m²
4) T'h= k0xT'v = 0,4264x74 = 32 kN/m²
k0= (1-sen35) = 0,4264
5) Th= T'h + u
Th= 32 +40 = 72 kN/m²
Para responder essa
pergunta devemos colocar em prática nosso conhecimento sobre Mecânica dos
Solos.
Para solos saturados, a tensão
efetiva vertical (σv,ef) é definida como a diferença
entre a tensão total vertical (σv) e a pressão neutra (u)
exercida pela água, também chamada de poropressão. Matematicamente, escreve-se
que:
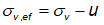
A tensão total vertical
em um ponto X é calculada por meio da soma dos produtos entre a altura de
camada de solo acima de X e o respectivo peso específico do material; e que a poropressão
em um ponto X é calculada pelo produto entre a diferença de cota do ponto X
e a cota do nível de água, e o peso específico da água (10 kN/m³). Logo, na
cota - 6 m, tem-se que:
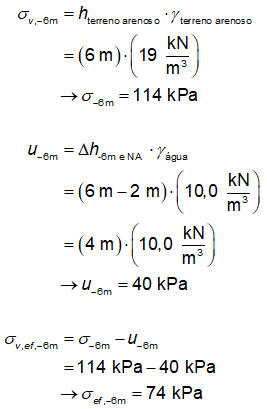
Portanto, a tensão efetiva
vertical total é de 74 kPa.
Por sua vez, a tensão
horizontal total efetiva (σh,ef) é calculada por meio da equação abaixo:
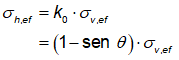
Em que θ é o ângulo de atrito interno do solo.
Logo, para o problema em questão:

Por fim, analogamente ao
calculado para a tensão vertical, a tensão horizontal total (σh)
é a soma da tensão horizontal efetiva com a poropressão. Desse modo:
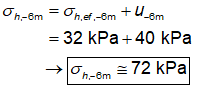
Logo, as tensões
horizontais totais e efetivas na cota - 6m são, respectivamente, 72 kPa
e 32 kPa. Com isso, tem-se que a alternativa A está correta.
Gabarito do professor: Letra A.