Questão 792532

• Banca: ESAF
• Órgão: Receita Federal
• Ano: 2012
• Provas: ESAF - 2012 - Receita Federal - Auditor Fiscal da Receita Federal - Prova 1 - Gabarito 1
• Disciplina: Matemática
• Assuntos: Estatística

A expectância de uma variável aleatória x - média ou esperança matemática como também é chamada - é igual a 2, ou seja: E(x) = 2. Sabendo-se que a média dos quadrados de x é igual a 9, então os valores da variância e do coeficiente de variação de x são, respectivamente, iguais a

• A. 5; (^√5⁄₂)
  
  
• B. 5; √5.
  
  
• C. √5;  ^√2⁄₅.
  
  
• D. √5;  ²⁄_√5.
  
  
• E. (^√5⁄₂); 5.
  
  

Gabarito: A

Comentários

• E(x) = 2    Expectância de uma variável aleatória x ? média ou
  esperança matemática ou valor esperado
  E (média dos quadrados de x) = E(X²) = 9
   [Variância de (x)]² = E(X²) – [ E(X)]² =  9 - 2²  = 9 – 5
    [Variância de (x)]²  = 5
   Para calcular o  coeficiente de variação de x (CVx) , temos que achar o desvio padrão de x (que é a raiz quadrada da variância).
   √(variânciax)² = √5
   desvio padrão de x = √5
   CVx = (desvio padrão de x) / E(x)
   CVx = (√5) / 2    
   Resposta letra  “ A “

• Para resolver essa questão nem precisa fazer a conta, basta saber os conceitos:
  
  Desvio padrão = raiz quadrada da variância (S = √S²)
  Coeficiente de variação = Desvio padrão/média (CV = S/x)
  
  Portanto, o segundo resultado deve ser igual à raiz quadrada do primeiro, dividido pela média, que é 2.
  Somente a alternativa A atende.

• Como vcs acharam a variância =5?  Alguém poderia explicar? 

• Pimenta's crew, há duas formulas básicas para se achar a variancia.

  1ª maneira- pegar os elementos e subtrair da média , elevar ao quadrado e depois dividir pelo número de elementos.

  -qual a variancia dos elementos 1,2 e 3? media=2

         S²={( x1-media do conjunto)²+( x2 -media do conjunto)²+( x3-media do conjunto)²}/3=

  (1-2)²+(2-2)²+(3-2)²=1²+0²+1²=2/3=0,66

  2ª maneira( usada na questão)- só que nesse caso eu não tenho os elementos e sim a média=2 e a média dos quadrados=9

  a formula diz q variancia é a media dos quadrados menos o quadrado da media= 9- 2²=5

  se tivesse os mesmos elementos acima(1,2 e 3) ficaria na formula abaixo

  •    s²= (x1² +x2²+x3²)/3- [(x1+x2+x3)/3]²= (1²+2²+3²)/3 -[(1+2+3)/3]²=(1+4+9)/3-2²=4,66-4= 0,66    

  • espero ter ajudado

• Aplicação direta de fórmula:

  Variância =média dos quadrados - quadrado da média

  Variância= 9 - (2)² = 9 - 4 = 5

   

  Coeficiente de variação (cv) = desvio padrão   *desvio padrão= √variância

                                                    média

  cv = √5

          2

  Resposta: letra a)

                                          

• Foi dito que E(X) = 2, e que a média dos quadrados de X é 9, ou seja:

  

         A variância pode ser calculada por:

  Variância = E(X) – (E(X))

  Variância = 9 – (2) = 5

         Caso você não se lembrasse desta fórmula, poderia ter usado:

  

         O desvio padrão é a raiz da variância, ou seja, 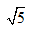. E o coeficiente de variação é:

  

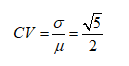
  Resposta: A

• RIP esaf

• GABARITO: A

  Média = E(x) = 2

  Média² = E(x²) = 9

  Outra jeito de fazer o calculo da variância (σ²) = E(x²) - [E(x)]² --> σ² = 9 - (2)²

  σ²= 9 - 4 = 5

  Agora calcule o Desvio-Padrão (σ) --> σ = √(σ2) --> σ = √5

  Agora calcule o Coeficiente de variação (CV) = Desvio-Padrão (σ) / Média

  Coeficiente de variação (CV) = √5 / 2