-
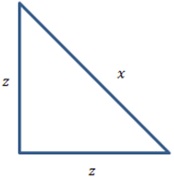
Trata-se de um triângulo isósceles ( Dados da questão: é triângulo um retângulo (90o) com um dos ângulos medindo 45o, ou seja o terceiro também 45o ).
Conclui-se que esse triângulo tem dois lados iguais: Z e W-2= Z
O Seno de 45o = cateto oposto/ hipotenusa
√2 / 2 = cateto oposto/ hipotenusa
√2 / 2 = Z / hipotenusa
Hipotenusa = Z.√2
Os lados do triangulo são: Z + Z + Z√2 = 2Z + Z√2 ( Perimetro do triangulo ) Gab letra " E "
-
ERALDO.. consegui acompanhar tua linha de raciocinio até esta parte:
-----------------------------------------------------------------------
√2 / 2 = Z / hipotenusa
Hipotenusa = Z.√2
-------------------------------------------------------------------------
não consegui entender como sumiu o "2" e como que a "√2" passou multiplicando...
pelos meus calculos ficaria assim:
√2/2 = Z / hipotenusa
2 Z = hipotenusa √2 (passava o √2 multiplicando para o outro lado dividindo)
2 Z / √2 = hipotenusa.
se alguém puder explicar melhor essa parte eu agradeceria.
-
Explicando melhor a resolução da questão
√2. Hipotenusa = 2.Z
Hipotenusa = 2.Z / √2 (Para racionalizar fracções em que o denominador e uma raiz quadrada, multiplicamos ambos os termos da fração por essa mesma
raiz quadrada e, assim, obtemos uma fração equivalente com denominador radical).
Hipotenusa = = 2.Z. √2 / √2. √2 ( √2 . √2 = √22 = 2 )
Hipotenusa = 2. Z.√2 / 2
Hipotenusa = Z.√2
Os lados do triângulo são: Z + Z + Z√2 = 2Z + Z√2 ( Perímetro do triângulo ) Gab letra " E "
-
fico muito agradecido camarada, eu realmente tinha me esquecido da racionalização.
bons estudos
-
NÃO ENTENDE PORQUE TRIANGULO ISÓCELES?
-
é isóceles pois se temos um triângulo retângulo já sabemos que ele possui um ângulo de 90º. Como o enunciado diz que ele tem mais um interno de 45º, restam mais um de 45º para fechar os 180º. Lembre-se: a soma dos ângulos internos de um triângulo é 180º
-
Pessoal,
1) Triângulo Retângulo => Um ângulo interno é reto ( 90 Graus) e os outros dois são agudos ( ângulos entre 0 e 90 graus). Os lados que determinam os ângulos retos chamam-se Catetos do triângulo e o lado oposto ao ângulo reto chamamos de hipotenusa.
2) A soma dos ângulos internos de um triângulo é sempre 180 Graus.
3) Se observarmos neste exercício temos 1 ângulo reto = 90 graus ( triângulo retângulo) e no enunciado diz que um dos ângulos internos é 45 Graus, logo, se somarmos 90 + 45 + X = 180, teremos que X = 45 Graus.
4) Se olharmos a definição de um triângulo isósceles: Tem 2 lados iguais. O teceiro lado chama-se base. Para todo triângulo isósceles valem as seguintes propriedades: a) Os dois ângulos adjacentes à base são iguais; b) A mediana traçada em relação à base é também altura e bissetriz interna.
5) Logo nosso exemplo passou de triângulo retângulo para triângulo isósceles devido ao apresentado acima.
6) Então, resolvendo a questão temos que W-2 = Z, então usaremos Z para facilitar os cálculos.
7) Lembrando que seno 45 graus = cós 45 graus = √2/2, temos:
8) Sem 45 = Cateto Oposto / Hipotenusa => Hipotenusa = Cateto Oposto * √2/2, teremos H= Z * √2/2
9) Então o perímetro será a soma dos 2 catetos + hipotenusa
10) ( Z*√2/2 ) + Z + Z , Logo temos (Z*√2 / 2) + 2Z => tirando o mmc = 2, temos: Z*√2 /2 + 4Z/2 => Z*√2 +2 Z e colocando Z em evidência, teremos: Z ( √2 + 2 ) ........letra “e”.
Espero que tenha ajudado...
Abraço a todos!
-
De acordo com o enunciado, temos um
triângulo retângulo, assim, um dos seus ângulos medem 90°. Sabemos pelo
enunciado que um dos ângulos internos vale 45°, como a soma dos ângulos
internos de um triângulo valem 180°, temos:
90° + 45° + y + 180° assim, y = 45°
Então temos um triângulo isósceles,
logo, dois de seus catetos são iguais, vamos chamar (w - 2) = z. Usando
Pitágoras:
x2 = z2 + z2 = 2z2 → x = z√2
-
MACETE
No triângulo retânglo isósceles, há 2 ângulos 45º e um reto(90º)
O macete é que os catetos serão iguais (exemplo = "x" ) e a hipostenusa será "x√2"
LOGO, nessa questão teremos catetos = z (como são iguais, vc usa o z pra facilitar o cálculo) e hipotenusa = z√2
perímetro é a soma dos lados = z + z + z√2
= 2z+√2
=z (2 + √2)
Sabendo essa propriedade do triângulo retângulo isósceles não precisa calcular hipotenusa, nem seno, nem cosseno, nem fração, nem MMC. basta pensar um pouquinho.
-
Temos a seguinte disposição:

Veja que:
tan(45º) = (w – 2) / z
1 = (w – 2) / z
z = (w – 2)
Veja ainda que:
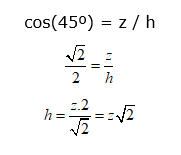
Portanto, o perímetro desse triângulo, em metros, é igual a:

Resposta: E
-
http://humexatas.blogspot.com/2017/09/resolucao-esaf-2012-receita-federal_25.html
CATETO 1 = Z METROS
CATETO 2 = (W-2) METROS
PERÍMETROS=
Z+(W-2)+X =
Z+Z+Z√ 2 =
2Z+Z√2 =
Z(2+√2)