-
São equivalentes pois as tabelas verdade só iguais:
P-> Q ~Q->~P
V V
F F
V V
V V
-
Luiz joga basquete representando por P
Luiz é alto representado por Q
Luiz não joga basquete representado por ~P
Luiz não é alto representado por ~Q
Logo temos: P-->Q é equivalente a ~Q-->~P. Interesse observar que "-->" é representado por "porque" que se equipara a "então". Sendo assim, é perfeitamente possível a representação por "-->".
Avante!!!!!!!!
-
Esse é um caso de equivalência de contrarrecíproca, onde, P --> Q equivale a ~Q --> ~P
-
A = LUIZ JOGA BASQUETE
B = LUIZ E ALTO
Luiz joga basquete porque Luiz e alto
A -> B
Luiz nao e alto porque Luiz nao joga basquete
~A -> ~B
A -> B = ~A -> ~B
Resposta: Certa
-
Tem que perceber que o "porque" equivale ao "então."
-
CERTO
Apenas complementando...
TABELA DE EQUIVALENCIAS
P ^ Q |
Q ^ P |
P v Q |
Q v P |
P --> Q |
~Q --> ~P
~P v Q |
P <--> Q |
P --> Q ^ Q --> P |
-
esta e a equivalencia contrapositiva!
-
uma dica
para gravar: volta negando
P →Q é equivalente ~Q →~P
-
"Luiz joga basquete porque Luiz é alto", leia-se:
Luiz ser alto é condição necessária para Luiz jogar basquete = p-->q
OU
Uma condição necessária para Luiz jogar basquete é Luiz ser alto = p-->q
-
Se Luiz joga basquete B:
Então Luiz é Alto A:
Se Luiz não é alto ~A:
Então Luiz não joga basquete ~B:
Jogando na tabela verdade
A B ~B ~A B-->A ~A-->~B
V V F F V V
V F V F V V
F V F V F F
F F V V V V
Portanto são logicamente equivalentes
-
Ninguém até agora comentou que a leitura deve ser invertida.
Se a questão diz que "Luiz joga basquete porque é alto", Luiz jogar basquete é consequência dele ser alto. Primeiro ele é alto, depois ele joga basquete. Logo, se a frase for transformada para o conectivo Se...Então, deve ficar assim: Se Luiz é alto, então ele joga basquete (e não o contrário, como colocaram).
No fim das contas, nessa questão, vai dar no mesmo, porque Q→P também é equivalente a ~P→~Q. Mas a tradução da linguagem corrente para a simbólica frequentemente é objeto de avaliação.
-
Perfeito o comentário do colega acima. Usa-se a mesma ideia em QUANDO e POIS.
Deus é Pai
-
P-->Q = ~Q-->~P
Q = Luiz é Alto
P = Luiz joga basquete
Negando( Luiz é Alto) fica (Luiz não é Alto)
Negando(Luiz joga basquete)fica(Luiz não joga basquete)
Correta!
-
Pessoal, me perdoem pela ignorância...
Eu realmente não sei nada de RL e com muita dificuldade estou tentando aprender!
Ao fazer a tabela verdade a minha resolução deu diferente, se alguém puder me ajudar a identificar o erro:
P --> Q ~P --> ~Q
V V
F V
V F
V V
A resolução da ~P --> ~Q ficou assim:
F --> F V
F --> V V
V --> F F
V --> V V
O que eu fiz de errado???
-
Cara colega Juliana:
a construção correta, de acordo com o teorema do contrarrecíproco, é:
P ---> Q ========> ~Q ---> ~P
V V
F F
V V
V V
Como se pode notar, ambas as tabelas são iguais. Portanto são logicamente equivalentes.
Obs.: Esse teorema do contrarrecíproco é exclusivo do se... então.
Bons estudos.
Inté.
-
eu não entendo muito desse assunto e nem sei fazer esses calculos. posso parecer ignorante, mas de qualquer jeito vou postar aqui minha opinião e porque eu acho que está ERRADA. me corrijam por favor. eu acho que é falso pq na primeira proposição entende-se que: '' Se Luiz é alto, então ele jogará basquete''. E na segunda proposição está dizendo que: ''Luiz NÃO é alto POIS não joga basquete. Logo, se ele jogasse basquete, ele seria alto.'' E isso não faz sentido, alem de estar descordando da primeira
-
A questão é simples, todavia você tem que saber a equivalência do --> (se...então...)
Se Luiz joga basquete, então Luiz é alto.
A: Luiz joga basquete
B: Luiz é alto
Há duas equivalência do --> (se...então)
A --> B = (Se Luiz joga basquete, então Luiz é alto)
a) ¬B --> ¬A = (Se Luiz não é alto, então Luiz não joga basquete)
b) ¬A v B = (Luiz não joga basquete ou Luiz é alto)
Espero ter ajudado.
Bons estudos.
-
Inverte e nega, umas das formas de se achar a equivalência de uma condicional.
-
Quando, como, portanto, logo, pois, porque são CONDICIONAIS.
“Luiz joga basquete porque Luiz é alto” = A -> B
e “Luiz não é alto porque Luiz não joga basquete” = ~ B -> ~ A
Regra do "NEGIN" para encontrar proposições condicionais equivalentes.
NE|go as proposições e In|verto.
Tirando a prova:
| A | B | ~ A | ~ B | A -> B | ~ B -> ~ A |
| V | V | F | F | V | V |
| V | F | F | V | F | F |
| F | V | V | F | V | V |
| F | F | V | V | V | V |
Gabarito CERTO.
-
Felipe, esqueca o significado da proposicao, grave apenas as regras de equivalencia e negacao.
-
Grave os conectivos, mas grave uma coisa: as questões de lógica do Cespe são ardilosas. O examinador faz um jogo de compreensão e simbologia.
-
É sabido que as seguintes palavras (quando,
como, portanto, logo, pois, porque) caracterizam uma proposição Condicional.
Assim, podemos reescrever as proposições da seguinte maneira:
P1: “Luiz joga basquete porque Luiz é
alto” = A → B
P2: “Luiz não é alto porque Luiz não
joga basquete” = ~B →
~A
Onde:
A = Luiz joga basquete
B = Luiz é alto
Fazendo a tabela-verdade:
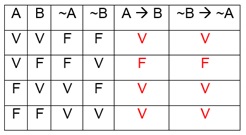
Logo
vemos que as colunas entre as proposições são iguais, configurando uma
equivalência entre as proposições.
RESPOSTA: CERTO
-
A → B = ~B → ~A
-
Porque conjunção que indica causa, então grave "porque" = "se, então" agora fica mais simples compreender e você acerta tudo. Depois disso houve só a inversão denominada na lógica de modus tollens: troca de lado e inverte os sinais e você terá a equivalência lógica entre as proposições, assim: A → B = ~B → ~A.
Bons estudos.
-
Questão ardida!!!!
-
Só trocar o "porque" por "então" e usar uma das equivalências da condicional: inverte e nega.
P ---> Q
~Q ---> ~P
Se Luiz joga basquete então Luiz é alto
Se Luiz não é alto então Luiz não joga basquete
-
Reescrevendo as proposições:
"Luiz joga basquete(consequência) porque Luiz é alto (causa)" = "Se luiz é alto então joga basquete"
Equivalência: "Se luiz não joga basquete (causa) então luiz não é alto (consequência)" = “Luiz não é alto (consequência) porque Luiz não joga basquete (causa)”
-
GABARITO CERTO
Há anos o CESPE adota o termo "pois" como condicional invertida, portanto:
“Luiz joga basquete porque Luiz é alto” (P --> Q), utilizando a condicional invertida teremos "Se Luiz é alto, então Luiz não joga basquete" (Q --> P). Observe que eu NÃO NEGUEI apenas inverti!
“Luiz não é alto porque Luiz não joga basquete” (~Q --> ~P) mesmo processo utilizado acima, ou seja, condicional invertida "Se Luiz não joga basquete, então Luiz não é alto" (~P --> ~Q).
Depois de invertida observe que as proposições ficaram da seguinte forma: (Q --> P) que terá como equivalência (~P --> ~Q)
-
Outras formas de condicional além de PORQUE e POIS : > QUANDO, TODA VEZ QUE , SEMPRE QUE.
-
QUESTÃO FÁCIL SE VC CONHECE A TABELA DA VERDADE
PROPOSIÇÕES (UMA DICA - O NÚMERO DE PROPOSIÇÕES GERALMENTE É O NÚMERO D VERBOS - MAS CUIDADOS COM AS ELIPSES VERBAIS) :
1) Luiz joga basquete (LJB)
2) Luiz é alto (LEA)
A RELAÇÃO É CONDICIONAL (P --> Q), UMA VEZ QUE LJB PORQUE LEA ====> LJB --> LEA
UMA DAS EQUIVALÊNCIAS DA TABELA É QUE (P-->Q = ~Q --> ~P) OU SEJA:
~LEA --> ~LJB
TRADUZINDO:
Luiz não é alto (~LEA) porque (-->) Luiz não joga basquete (LJB)
-
A -> B
~B -> ~A (Equivalente da condiciconal)
-
Luiz joga basquete porque Luiz é alto = P--->Q
Luiz não é alto porque Luiz não joga basquete = ~Q--->~P (contrapositiva da condicional)
Obs.: o ''porque'' funciona como uma condicional, se...então...
Questão correta, pois são logicamente equivalentes!
-
"Luiz joga basquete porque Luiz é alto" = Se Luiz joga basquete,então Luiz é alto
Equivalência de p->q é ~q->~p e também ~pvq
Temos a equivalência:
Se Luiz não é alto,então Luiz não joga Basquete= "Luiz não é alto porque Luiz não joga basquete"
-
A Única dificuldade que senti foi que eu não sabia que o PORQUE tinha significado de SE ENTAO
VOLTANDO NEGANDO QUE DA TUDO CERTO !
-
O "pois" e o "porque" são a mesma coisa que o "Se.. então"
Ressalva quanto ao "porque" e o "pois", nestes dois casos a proposição é feita a partir do inverso da linguagem comum que utilizamos
Jose passou pois ele estudou = se jose estudou, então ele passou.
Equivalência da condicional é o Neymar, ~P V Q
Negação é exatamente o inverso da equivalência, então se tu vai negar a equivalência tu vai inverter o V da equivalência ficando "Equi^alência" mas pra ficar mais fácil, então vamos ao macete. Ne-ga-ção, separação silábica. Perceba que o tio "~" está na parte final palavra, então o tio também ficará na parte final da proposição. Resultado em P ^ ~Q.
Parece besteira a negação certo? mas ela me salvou em uma prova exatamente por confundir a equivalência com a negação.
-
P ---> Q
~Q ----> ~P
Inverte negando ambas.