-
A probabilidade de escolhermos um (primeiro) infrator é...
2/10=1/5
E
Agora escolhendo o segundo a probabilidade será...
1/9
Logo; 1/5*1/9=1/45=0,022222.... ou ~2,222%
SUPERIOR A 2%... RESPOSTA ERRADA!
ATÉ MAIS!
;)
-
Outro modo de resolver a questão, utilizando a Combinação Simples:
C(n,p) = n! / p!(n-p)!
1- Primeiro, descobrimos quantas formas existem de escolher 2 postos aleatoriamente: C(10,2)
C(10,2) = 10!/2!(10-2)! = 10x9x8!/(2x1)x8! = 10x9/2 = 90/2 = 45
Assim, existem 45 maneiras diferentes de escolher 2 postos aleatoriamente, estas maneiras correspondem a 100%
2- Sabemos que só há 1 possibilidade de escolhermos 2 postos infratores em um grupo de 2, pois só existem 2 postos infratores na cidade.
3- Então, só precisamos saber quanto 1 possibilidade representa em relação ao universo de 45 possibilidades (100%):
Meios pelos extremos -> 45/1 e 100%/x -> 45x = 100 -> x=100/45 = 2,2222...
Logo, a probabilidade é superior a 2%
-
Escolher o primeiro = 2/10 E(mulTEplica) o segundo 1/9
2/10 * 1/9 = 2/90 , ou seja, se fosse 2/100 seria 2% como é "/90" então é maior que 2%.
-
Calculando-se
a probabilidade temos:

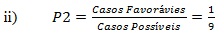
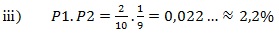
Errado.
-
galera me expliquem da onde vem esse 1/9 ?
eu fui apenas pela conta 2/10...
-
Luã, note que a probabilidade de esses dois postos serem os infratores, é de 2 em 10 postos, uma vez que saiu o primeiro posto, devemos então tirar um da lista, lista que de 10 postos passa agora para 9 postos.
Daí continuamos, agora precisamos só de mais 1 posto para completar o que queremos, então temos chance de conseguir 1 em 9 postos restantes.
Após isso é só multiplicar e fazer como os colegas mencionaram.
Bons estudos.
-
Probabilidade= Casos Favoráveis(O QUE EU QUERO)/Casos Possíveis (TOTAL)
P=2/10 * 1/9 ( Como so tenho 2 casos favoráveis e já usei 1 diminuiu do total tb)
Prefiro dividir 2/10= 0,2 | 1/9= 0,11
Pegue os resultados é multiplica 0.2x0.11= 0,022=> 2.2%
Maior que 2% Errada Questão.
Boa Sorte.
-
GABARITO:ERRADO
PROBABILIDADE
2/10 X 1/9= 2/90
A questão afirma que 2/90 é menor que 2/100, e com numeradores iguais o maior número é aquele com menor denominador, exatamente o contrário que a questão propõe
-
Acredito que essa seja a forma mais rápida de calcular numa prova (sem calculadora):
Primeiro posto: 2/10 e Segundo posto: 1/9
2/10 * 1/9 = 1/5 * 1/9 = 1/45
A questão sugere que seja inferior a 2%, que é igual a 2/100 = 1/50
Ou seja, 1/45 > 1/50. Questão errada.
-
GABARITO ERRADO
O total de maneiras de se escolher 2 postos em 10 é: C(10,2) = 10 x 9 / (2 x 1) = 45
O total de maneiras de se escolher 2 dos 2 postos infratores é: C(2,2) = 1
Portanto, a probabilidade de escolher exatamente dois postos infratores é: P = 1 / 45 = 0,0222 = 2,22%
FONTE: Prof. Arthur Lima
"Se não puder se destacar pelo talento, vença pelo esforço"
-
Fiz por arranjo, se for uma forma errada de resolver, avise- me por mensagem por favor.
- Bom, como faz diferença se eu pegar 1 posto irregular e outro regular, usei arranjo para calcular o total de possibilidades:
- A10,2 = 90
- Probabilidade de escolher os dois dentre os 90 = 2 / 90 = 0,0222... = 2,22% > 2%
GABARITO: ERRADO
-
Ok, eu raciocinei da seguinte forma: Tenho 10 postos, desses 10, dois são infratores. A questão quer saber seeeeeee é inferior a 2% a probabilidade de eu escolher aleatoriamente dois desses 10.
1°, Pego esses 10 e vejo de quantas formas posso combiná-los(Pra isso eu entro em combinação): C10,2 :. 10!/(10-2)!x2! R: 45 formas de combiná-los!
ok!
2° Das 45 formas de combiná-los, há uma única possibilidade de tirar os dois juntos de uma única vez. Sabe pq? Pq só há dois postos infratores. Ou vc tira os dois juntos ou tira um infrator e um não infrator.... ooooou não tira caralha nenhuma de infrator! Sacou? Se vc entender isso daqui, vc é genial e pode sacar qualquer coisa! Pra mim, esse é o "X" da questão(seguindo minha linha de raciocínio).
3°, Tenho uma única possibilidade de ter os 2 juntos, dentro de um espaço amostral de 45. Ou seja: 1/45 R=0,0222222....
É muito bizarro olhar pra isso e dizer, caraleo, consegui! Se eu consigo, vai por mim, tu tambm consegues!!!!
Qualquer erro cê me manda em inbox!!!