-
I) A média dobra. --> CORRETO;
É calculada pela soma de todos os salários dividido pelo número de assalariados. Ao dobrar cada salário, a média aritmética também dobra.
II) A variância dobra. --> ERRADO
A variância, que é soma dos quadrados dos desvios dividida pelo número de ocorrências (média do quadrado dos desvios), quadruplica quando a média dobra. Ou seja, se os desvios dobram de valor quando os salários dobram, seria como pegar uma coisa que dobra de valor e elevá-la ao quadrado.
III) A moda dobra --> CORRETO
A moda se refere aos valores de salários mais comuns (valores mais recorrentes). Se todos salários dobram o valor referente à moda também dobra.
Variância no Wikipedia: Em linguagem comum isto pode ser expresso como "A média do quadrado da distância de cada ponto até a média". É assim a "média do quadrado dos desvios".
Desvio Padrão é a raiz quadrada da variância. Neste caso o desvio padrão varia com o fator 2, assim como a média e a moda.
-
Tomando como exemplo três funcionários que ganhavam 1, 2, 3.........salário dobrado 2, 4, 6
salário atual somado = 6
salário dobrado somado = 12
I - média atual = 6/3 = 2............................média dobrada =12/3 = 4
correta, média dobra.
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
II - variância fórmula -> var=(x1 - x*)² + (x2 - x*)² + (x3 - x*)² OBS: onde x* é a média aritmética simples entre os termos e N números de termos N - 1
com o exemplo acima ficaria assim:
var = (1 - 2)² + (2 - 2)² + (3 - 2)² = 1 + 0 + 1 : 2 = 1
3 - 1
com salário dobrado
var = (2 - 4)² + (4 - 4)² + (6 - 4)² = 4 + 0 + 4 : 2 = 4
3 - 1
Errada, nunca dobra.
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
III - Resposta conforme a do colega abaixo.
-
Questão meio confusa, nem sempre a moda dobraria:
Salário por ex: 600, 600, 1200, 1200 = não há moda, se não há moda, como vai dobrá-la?.
Se alguém conseguir me explicar a III ser verdadeira de uma forma diversa, ficaria muito agradecido!!!
-
Max, moda é o que mais se repete, no caso aí tem dois 600, então a moda é 600.
-
Quando a questão fala em dobrar, seria o valor x e não a quantidade.
Seguindo o exemplo do Max quando o exercício diz que a moda dobra, ele quis dizer que a moda passaria a ser (1200,1200,2400 e 2400) e no mesmo exemplo do Max, existe moda SIM. É um exemplo bimodal, ou seja, com duas modas, não necessariamente para se ter uma moda precisa ter apenas um único conjunto se repetindo mais vezes..
-
Segue abaixo uma tabela com o resumo das propriedades da Média, Moda, Mediana, D.A.M, Desvio Padrão e Variância:
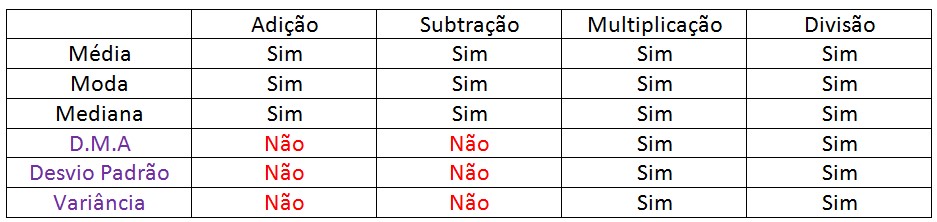
Logo, vemos que as medidas de posições são influenciadas pelas quatro operações enquanto que as medidas de dispersões são influenciada apenas pela multiplicação e divisão.
Observação: Devemos lembrar que a variância é influenciada pelo quadrado do número que a está multiplicando. Ou seja, se o salário for multiplicado por 2, a variância quadruplica (2² = 4).
Assim, tendo em mãos estas informações, concluímos que apenas a Média e a Moda dobrarão.
Resposta: Alternativa C.
-
Concordo com o raciocínio do Max... No exemplo que ele deu 600,600, 1200,1200 não há moda, é um conjunto AMODAL... logo se não há moda, não posso afirmar que a moda irá sempre dobrar. A questão não falou os valores dos salários, logo poderia existir o caso de todos os funcionários terem salários diferentes...
-
Marcelo, como o colega abaixo já explicou, existe moda sim. São duas modas. isso é possível.
-
Ao dobrar cada salário a média dobra.
Se a média dobra, a variância quadruplica.
Ao dobrar todos os salários a moda dobra.