-
Total = 1000
280 ----- > tecnologia T
400 ------ > saude S
600 ------ > humanidades H
T + S + H = 1280, porém só existem 1000 alunos, logo 280 fazem 2 matérias.
Temos:
Alunos que fazem T e S
Alunos que fazem S e H
Alunos que fazem H e T
Sabendo que a quantidade de estudantes que fazem S e H é igual ao dobro da quantidade dos que realizam cursos das áreas de H e T que, por sua vez H e T, é igual ao dobro dos que fazem cursos das áreas de T e S, a quantidade de entrevistados que fazem apenas cursos da área de tecnologia é igual a:
Veja que um é o dobro do outro, então o primeiro é 4x maior que o último.
Vamos chamar todas as combinações de x
4 X + 2 X + X = 280 ---- > X = 40
Voltando nos alunos que só fazem Tecnologia: SóT = T - (TeS + HeT) ------ > SóT = 280 - (80 + 40) ------- > SóT = 160 letra B
-
Fazendo
o diagrama de Venn:
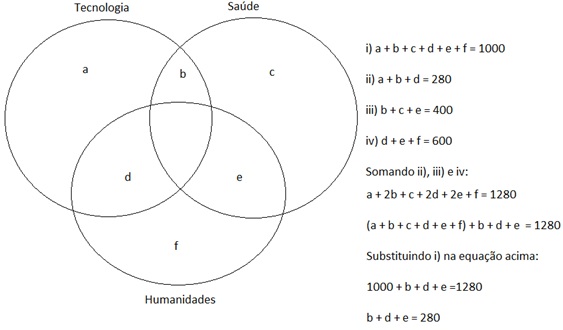
De acordo com o enunciado, a
quantidade de estudantes que fazem cursos das áreas de humanidades e saúde é
igual ao dobro da quantidade dos que realizam cursos das áreas de humanidades e
tecnologia que, por sua vez, é igual ao dobro dos que fazem cursos das áreas de
tecnologia e saúde, temos:

-
Alana, não entendi como vc chegou à conclusão: "Veja que um é o dobro do outro, então o primeiro é 4x maior que o último."
Sendo que: "Sabendo que a quantidade de estudantes que fazem S e H é igual ao dobro da quantidade dos que realizam cursos das áreas de H e T que, por sua vez H e T, é igual ao dobro dos que fazem cursos das áreas de T e S"Se puder me explicar, agradeço!
-
Simples Marina Corbucci, veja:
"Sabendo que a quantidade de estudantes que fazem cursos das áreas de
humanidades(H) e saúde(S) é igual ao dobro da quantidade dos que realizam
cursos das áreas de humanidades(H) e tecnologia(T) que, por sua vez, é igual
ao dobro dos que fazem cursos das áreas de tecnologia(T) e saúde(S)"
Esse trecho da questão versa sobre as interseções entre SxH, HxT e TxS. Podemos chamar TxS de "X", a partir daí(seguindo o trecho da questão supracitado) temos que HxT é o dobro de TxS, portanto "2X" e finalmente que SxH é o dobro de HxT, logo 2.2x=4x.
A partir daí temos:
4 X + 2 X + X = 280(alunos que fazem mais de um curso) ---- >fazendo as contas, X = 40;
Como a questão pede somente o valor de "T", vamos fazer as contas:
280 -2x -x
280 (-2.40) -40
280 -120 = 160. ==> Nossa resposta.
Espero ter ajudado.
-
a + b + c + T + S + H = 1000
a + b + T = 280 (I)
b + c + S = 400 (II)
a + c + H = 600 (III)
Soma de (I) + (II) + (III):
(a + b + c + T + S + H) + (a + b + c) = 1280
a + b + c = 280 (IV)
c = 2.a
a = 2.b
Substituir em (IV):
a + (a/2) + 2a = 280
2a + a + 4a = 560
7a = 560
a = 80
b = 80/2 = 40
c = 2.80 = 160
Equação (I):
80 + 40 + T = 280
T = 280 – 120
T = 160 --------------------- Alternativa (B)
http://mathsconcursos.blogspot.com.br/2015/07/inss-11012009.html
-
Primeiro vamos saber o valor das interseções
1000 = 280 + 400 + 600 - X
X = 280
Feito isso basta fazer uma divisão diretamente proporcional, veja:
Vou chamar H^S de A, H^T de B e T^S de C e darei valores a cada um ficando assim
A = 4 (dobrei o valor de B)
B = 2 (dobrei o valor de C)
C = 1 (sendo esse o menor valor, então coloquei o menor valor possível)
Agora só basta dividir o número 280 por partes diretamente proporcionais a 1, 2 e 4, vamos encontrar os valores 40, 80 e 160, agora é só colocar no diagrama e partir para o abraço.