-
A=ATIVIDADE I, B= ATIVIDADE II , C= NENHUMA DAS DUAS ANTERIORES, E X A POSSÍVEL INTERCECÇÃO DE a A E B
A=29-X
B=28-X
C=Y
(29-X) + (28-X) + Y = 35
Y=X - 22
COMO ELE QUER O MAIOR VALOR DE Y, X TEM QUE ASSUMIR O MAIOR VALOR POSSÍVEL, E ESSE VALOR É 28 JÁ QUE B=28-X E B NÃO PODE SER NEGATIVO, SENDO ASSIM, Y=28-22= 6
-
olhem só
Atividade I tem 29 que gostam
Atividade II tem 28 que gostam
fazendo um desenho pra ficar melhor para visualizar teremos
___Universo(total, que é igual a 35 pesquisados)_____|
| ___Ativ I__________Ativ II__| |
| | | | | |
| | 29-X | X | 28-X | |
| |_______|____|_________| Y |
| |
|___________________________________________|
Espero que de para entender. X é a quantidade de pessoas que gostam das duas atividades e Y são as pessoas que não gostam de nenhuma das duas atividades.
Pelo desenho X tem que ser menor que 28, pq se fosse maior, o numero de pessoas que gostariam da atividade 2 daria negativo, o que é impossivel.
Somando as partes 29-X(pessoas que gostam somente da atividade I) com x (pessoas que gostam das 2 atividades) com 28-X (pessoas que gostam so da atividade II) com Y ( pessoas que não gostam de nenhuma das atividades) teremos o total, que é 35 entrevistados
vamos lá! (29-x) + X + (28-X) + Y = 35 ----> 57 -x +Y =35 -----> x-y= 22 portanto, y=x-22
se y=0, teremos o menor X possível que será 22 e no máximo 28 como vimos anteriormente.
farei uma tabela para visualizar melhor
Atividade I Gostam das 2 Atividade II Não gostam de nada
29-x x 28-x y=x-22
29 -22 =7 22 28-22=6 y=22-22=0
29-23=6 23 28-23=5 y=23-22=1
29-24=5 24 28-24=4 y=24-22=2
29-25=4 25 28-25=3 y=25-22=3
29-26=3 26 28-26=2 y=26-22=4
29-27=2 27 28-27=1 y=27-22=5
29-28=1 28 28-28=0 y=28-22=6
portanto o maximo que y(pessoas que não gostam da atividade I ou II) será 6. A afirmação está correta
-
Resumindo:
São 35 técnicos e 2 pesquisas.
I - 29 gostam
II - 28 gostam
Diagrama:
I (29) II (28)
--------------------------
| | | |
| 1 | 28 | |
| | | |
--------------------------
Ou seja, se eu colocar os 28 na interseção e 1 em "apenas A" eu tenho de sobra 6 (35-29) que é o máximo que pode ficar fora e ainda assim estará satisfeita a relação no diagrama.
-
Fiz a questão raciocinando da seguinte forma : (sei que não daria certo para todas as questoes parecidas, mas só em algumas)
Se 29 gostam da atividade I já posso descartar 29 do total pois 29 gostam de ao menos uma atividade.
Sendo assim, já teriamos o valor menor que seria (35-29=6). não havendo possibilidade de ser superior a 7 o numero de tecnicos que nao
gosta de nenhuma atividade.
Se estiver errada, alguem esclareça para mim.
-
Teoricamente, é mais complicado, mas, na prática é bem simples.
Universo = 35
Se 29 gostam de, pelo menos uma atividade, então, na pior das hipóteses ("o maior número possível de técnicos que não gostam de nada"), teríamos 6 que não gostam de nenhuma atividade.
35-29=6
-
A resolução do Mateus Pereira segue um raciocínio excelente, porém ele deixou de inserir na formula o X que é a intersecção entre os conjuntos A e B. Pois sem este valor seria impossivel se chegar a formula Y=X-22.
X+(29-X)+(28-X)+Y = 35
Y= 2X-X-22
Y= X-22
Bons Estudos!
-
Cespe sempre quebrando as pernas de quem sabe...
Li a questão e já imaginei que era inferior a 6 e não 7. Só que 6 é inferior a 7...
Acho que essa é a única banca que derruba os candidatos de todas as formas possíveis.
-
Alguem poderia me explicar porque tem que se adotoar o maio valor de x pra se conseguir o maior valor de y?
Eu até entendo que o maior de x é 28 porque não se pode ter um numero negativo de pessoas num dos grupos, mas porque isso leva ao maior valor de y?
-
total de técnicos 35
só gostam da atividade I = 29 - x
só gostam da atividade II = 28 - x
gostam das duas atividades = x
não gostam da duas atividades = y
logo, o total fica 29 - x + 28 - x + x +y = 35
calcula x - y = 22
agora começa a atribuir valores a y:
x-1=22 ...x=23
.
.
x-7=22 ...x=29
vc tem que perceber que qd x= 29 os que gostam da atividade I fica = 0 e os que gostam da atividade II ficará negativo
ver retomando o inicio da questao
só gostam da atividade II - 28 - x, troca o x por 29 dá igual a -1impossível. Tem que ser menor que 7.
-
Galera vem sempre com calculos mirabolantes. Mas lembrem-se: O CESPE FAZ ISSO PRA CANSAR O CANDIDATO! Tem SEMPRE uma maneira simples de resolver, SEMPRE! Concordo com o Luis Pereira!
-
Sinceramente, não vi ninguém, até agora, explicando a questão de forma lógica. Nada realmente objetivo.
-
35 é o total de técnicos.
29 gostam da atividade I
28 gostam da atividade II
Suponha que todos da atividade II gostem da atividade I
28 que gostam das duas atividades + 1 que gosta somente da atividade I = 29 gostam de alguma atividade
total de tecnicos - tecnicos que gostam de alguma das atividades = nao gostam de nenhuma atividade
35-29=6
-
Construindo o diagrama de Venn abaixo:
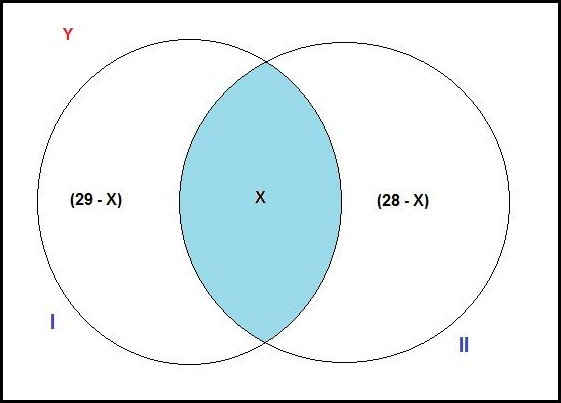
Montando-se agora a equação com o diagrama acima:
Y + (29 - X) + X + (28 - X) = 35 (total no grupo)
Resolvendo
Y = X + (35 - 57)
Y = X - 22
Assim para sabermos a quantidade máxima de técnicos desse grupo que não gosta de nenhuma das atividades, basta acharmos o valor máximo que a variável "X", pode atingir.
Para sabermos esse valor, basta olharmos o diagrama de Venn, no conjunto II. Ali vemos que o maior valor que "X" pode atingir é 28, qualquer valor acima deste, o conjunto II ficará com elementos negativos, o que não pode acontecer, assim:
Y = 28 - 22
Y = 6
Resposta: CERTO
-
OI PESSOAL, ALGUÉM SABE FAZER ESSA QUESTÃO ATRAVÉS DE DIAGRAMA?
ABRAÇOS ZENAIDE. PERNAMBUCANA, O FREVO COMENDO E EU ESTUDANDO RACIOCINIO LÓGICO. KKKKKKKK.
-
GABARITO CORRETO
35 entrevistados; 29 atividade1; 28 atividade2
a interseção tem que ser 22 que gostam das das duas atividades, pois tem-se 35 candidatos. até aí beleza!
agora quantos gostam exclusivamente; atividade 1= 29-22=7; atividade 2=28-22=6
a questão tá afirmando que a quantidade máxima de técnicos que se pode ter para não gostar de nenhuma das atividades é inferior a 7.
tem que ser pois se O máximo que se tem de membros gostando só de uma atividade são 7 membros da atividade 1, se for igual a 7 ou maior então se terá um conjunto vazio, porque se não gosta de um não tem jeito de gostar dos dois. em outra palavras:
se 6 pessoas não gostarem da atividade 2, ela esvaziará, mas ainda restará 1 da atividade 1.
-
Olá pessoal!
Bem, entendi da seguinte forma:
A questão afirma que a quantidade máxima de pessoas que não gosta de nenhuma das atividades é inferior a 7.
Vamos la
O universo é 35
U = 35
Os que gostam da atividade 1 é igual a 29
Os que gostam da atividade 2 é igual a 28
A soma de 28 + 29 será maior que meu universo, logo existem técnicos que gostam de ambas as atividades.
Vamos encontrá-los:
29 + 28 = 57
57 - 35 = 22 (estes são os que gostam de ambas as atividades)
Quem gosta somente da atividade I?
29 - 22 = 7 (técnicos que gostam somente da atividade I)
Quem gosta somente da atividade II?
28 - 22 = 6 (técnicos que gostam somente da atividade II.
Resolução:
Temos então que 22 gostam de ambas, 7 gostam da atividade I, 6 gostam da atividade II. Com isto temo o total do nosso Universo, ou seja, igual a 35. Logo temos o conjunto dos que não gostam de nenhuma das atividades como vazio, isto é, zero. Assim zero é menor do que 7.
-
Eu raciocinei da mesma forma que o Jansen
-
Gostaria de ajudar com o diagrama de Venn, mas nao consigo inserir figuras aqui.
Façam o seguinte: coloquem um círculo um dentro do outro, o de dentro chama de II e o de fora de I, ou seja 28 técnicos que gostam de II gostam também de I, mas no enunciado ele diz que 29 técnicos gostam de I então está faltando apenas 1, ou seja apenas um técnico gosta APENAS da atividade I, somando 28+1=29 como foram entrevistados 35 faça um círculo separado e coloque o numero 6 ou seja: 6 técnicos não gostam de nenhuma das atividades. 29+6=35. Faça os círculos, fica super fácil de entender.
Força Foco e Fé!!!
-
OLHA EU PENSEI ASSIM: CONSIDEREI A RESPOSTA DO ENUNCIADO COMO CORRETA, PORTANTO
28+29+7-X (INTERJEIÇÃO) = 35, TODAVIA TENDO COMO RESPOSTA 29, O QUE NÃO PODERIA OCORRER,
SENÃO TERÍAMOS UMA RESPOSTA NEGATIVA, LOGO RESPOSTA ERRADA.
-
Tentando ajudar...
1º Passo somar todo mundo e utiliza o 7 dado pela questão. Ele será o parâmetro da nossa resposta. E o que procuraremos? A intercessão!
29-x+x+28-x+7=35
64-x=35
-x-29
x=29
Achamos X=29. Como X é a intercessão, percebe-se que há algo de estranho. Como fica a atividade II? 28(atividade II) - 29(intercessão)= -1. Isso pode? Não!
E, se colocarmos 6 no lugar de 7? Ai sim. E como 6 <7. A resposta é CERTA.
Treine com exaustão até a perfeição.
-
35 - 29 = 6
29 gostam da Atividade 1.
28 gostam da Atividade 2. Logicamente, estes 28 também curtem a Atividade 1.
-
OLA, VOU SER OBJETIVO PARA VOCÊ ENTENDER
NA ATIVIDADE I TEMOS 29 TÉCNICOS QUE GOSTAM DELA
35-29= 6
NA PIOR DAS HIPÓTESES TEREMOS 6 TÉCNICOS QUE NÃO GOSTAM DE NENHUMA DAS ATIVIDADES.
-
Acho que dá pra entender né??
Vejam como é feita no diagrama: http://prntscr.com/655lr3
-
Meu raciocínio foi igual do, parceiro, JANSEN CARVALHO! ;) #rumoaosucesso
-
Vinícius Werneck , Matemático, Mestre e Doutorando em Geociências..
Pois é , mais aqui no QC não consigo entender direito uma explicação.
Professor , sugiro que faça videos respondendo algumas questões de raciocínio, porque essas explicações escritas não estão ajudando muito não!
grata!
-
Pessoal, quando abrirmos a aba acima para analisarmos o comentário do professor, vamos solicitar ao QC que coloque as explicações em vídeo aulas.
-
JANSEN CARVALHO o único que desvendou a questão nos comentários, para os recém chegados nem percam tempo, vão direto no comentário dele que é o correto.
-
Galera, a formula é a seguinte para se chegar à conclusão de que não há que não goste das atividades I e II:
A U B= A+B - A^B
-
Descontente com as explicações do professor, nuss, pqp, por mais que seja simples para vários usuários do site, para alguns não é.
Acredito que alguns vídeos explicando esse tipo de questão ajudariam mais que essas, textuais.
-
JANSEN CARVALHO (12 de Abril de 2014, às 14h57) para os recém chegados nem percam tempo, vão direto no comentário dele que é o correto.
-
Galera, vamos solicitar comentário em vídeo ao QC. Clique na -> aba do comentário do professor. -> não gostei.
irá aparecer pq vc não gostou?
-
Gente tô aprendendo raciocínio lógico a pouco tempo e talvez por isso não tente encontrar o então "pêlo em ovo" rsrsrsrs.
Simplesmente todos os 35 gostam de alguma das atividades então o máximo que não gosta de nada é ZERO, que é inferior a 7.
Pronto falei!!! rsrsr
-
Cara, tem que ser feita vídeo-aulas dessa disciplina...
-
Os comentários desse professor de Matemática são complexos demais. Em vez dele descomplicar, ele complica... Troquem de professor, pelo amor de Deus !!
-
Minha dificuldade aumentou depois de olhar o comentário do professor!!!
-
Pelo amor de Deus Q ... assim não dá...gravem vídeos como em Português, assim fica impossível, ninguém aqui entende o que o professor diz.
-
Atividade: 1= 29 2=28 para achar a interseção do conjunto é só somar ativ( 1+2) e pegar o conjunto universo, ou seja, 35, e subtrair, agora subtraindo 57-35, pronto achamos 22.
Bom 29-22 =7 28-22= 6
agora somando 7+6+22 temos 35 que fizeram alguma atividade. Bom se o meu total é 35, e eu sei que 35 fizeram alguma atividade, então subtraindo 35-35 temos, portanto, 0, ora 0 é menor que 7 ?, kkkkkkkkkk, claro que é. então
Gab: certo.
Espero ter ajudado, detesto o jeito de explicar RLM deses professor aqui do site.
-
Isso, a quantidade máxima de técnicos que não gosta de nada é = a 0, ou seja, todo mundo gosta de alguma coisa!!
-
Temos (29-X)+ X+( 28-X)+y=35
Temos a equação: y = X-22
temos que achar o valor máximo de y e o valor máximo de x. E como x é a interceção, o valor máximo precisar igual a 28, pois se fosse 29, teríamos -1 pessoas gostando de uma atividade (28-29).
Se X assumir o valor 28, teremos (29-28)+28+(28-28)= 29
Portanto: 35-29=6. Assim, o maior valor que x pode assumir é 28.
-
Equipe Q.C, ficaríamos satisfeitos se colocassem videos de resolução das questões de R.L.M / Matemática. Uma questão simples como essa acaba se tornando difícil quando lemos a explicação do Prof. por escrito. Vai a dica...
-
Resoluções em vídeos, pelo amor de Deus!!!!!
-
Em RL e algumas outras matérias, os comentários dos alunos são mais eficientes que a resposta dos professores.
QC, melhora aí!
-
29 gostam da atividade I, 28 da atividade II. logo somando as duas atividades ficam 57 Tec. mas existe apenas 35 no total. ou seja 57-35 = 22 que é a interseção do conjunto ou seja (22 Tec gostam da atividade I e da Atividade II), (7 gostam apenas da atividade I), e (6 gostam apenas da atividade II).(29 tec gostam da atividade I)
(28 tec. da atividade II)
Conclusão 29 TEC. gostam de algumas das duas atividades no total de 35 tec. logos 35-29 = 6 que não gostam de nenhuma atividade que é inferior a 7. gabarito ERRADO.
-
*****Um método diferente, resolvam pela resposta.
A=ATIVIDADE I, B= ATIVIDADE II
X= Intersecção de A e B (gostam de ambas atividades)
Y= Não gostam de nenhuma das duas atividades
A= 29 - X
B= 28 - X
Sendo (29-X) + (28-X) + X + Y = 35
----------------------------------------------------------------------------------------------
hipótese 1: Y = 7 (7 veio da afirmação da questão)
(29-X) + (28-X) + X + Y = 35
(29-X) + (28-X) + X + 7 = 35
-X + 64 = 35
X = 29 . Reparem agora, que se substituíssemos aqueles que gostam apenas da atividade II, ou seja, B, teríamos:
B = 28 - X
B = 28 - 29
B = -1. Ora, não podemos ter um número negativo de pessoas que não gostam da atividade II. Portanto, Y = 7 não é possível (assim como qualquer outro nº maior que 7, faça as contas se achar que deve).
----------------------------------------------------------------------------------------------
hipótese 2: Y = 6 (n° mais próximo inferior a 7, conforme afirmação da questão)
(29-X) + (28-X) + X + Y = 35
(29-X) + (28-X) + X + 6 = 35
-X + 63 = 35
X = 28 . Reparem agora, que se substituíssemos aqueles que gostam apenas da atividade II, ou seja, B, teríamos:
B = 28 - X
B = 28 - 28
B = 0. Ora, pode acontecer que ninguém goste somente da atividade II. Portanto, Y = 6 é possível (assim como qualquer outro número menor que 6, faça as contas se achar que deve). Assim, Y < 6, ou (conforme a questão) Y < 7. Gabarito correto!
-
Eu raciocinei assim: se 29 gostam da I, e 28 gostam da II, tem-se, com certeza que, no mínimo, 29 pessoas gostam de pelo menos uma das atividades. É o que dá pra concluir com precisão.
Ao contrário de alguns colegas aqui que disseram que o conjunto máximo de pessoas que não gostam de nenhuma atividade é igual a zero, eu penso que não, pois não tem como nós sabermos se realmente as 35 pessoas gostam de pelo menos uma atividade. Não dá pra termos certeza.
Pode ser que, das 35 pessoas, todas gostem de pelo menos uma das atividades. Mas pode ser que NÃO, ou seja, que algumas não gostem de nenhuma das atividades.
LOGO, o MÁXIMO de pessoas que pode não gostar de nenhuma é:
De 29 a 35 temos 6. Portanto, pode ser que ATÉ 6 PESSOAS não gostem de nenhuma das duas atividades.
Gabarito: correto (6 é inferior a 7)
-
se considerarmos B com somente 28 e que todos eles se encontrem na interceção de A com B , sobra somente 1 em apenas A e sobra 0 em apenas B .
-
escrevam não gostei e peçam vídeo, no comentário do prof.
-
Mônica Sátolo, excelente raciocínio! Realmente é a única coisa que se pode afirmar com certeza.
-
Encontrei a resposta. Se lerem devagar dá pra entender.
É assim: tem o conjunto da atividade I e tem o conjunto da atividade II
*Se são 35 entrevistados e 29 gostam da atividade I e 28 gostam da atividade II, bom, então: 28+29 = 57 e 57-30 = 22
*Então de início temos 22 que gostaram das duas simultaneamente.
*A questão diz que: A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
*Então temos que tirar elementos de dentro dos conjuntos e colocar do lado de fora, representando os que não gostam de nenhuma das duas atividades.
*de inicio ficaria assim:
*I →7 I e II→22 II→6 totalizando 35
Se tirarmos 1 elemento do conjunto I e colocássemos do lado de fora, teríamos que aumentar a interseção para 23, para manter a soma(29) dos que gostaram da atividade I, e diminuir a quantidade do conjunto II para 5, para manter a soma(28) dos que gostam da atividade II, dessa forma: 6 + 23 + 5 + 1 = 35. A partir daí continuamos a aumentar o numero dos que ficaram do lado de fora, ou seja, dos que não gostam de nenhuma das atividades.
*(I →6 I e II→23 II→5) + 1 totalizando 35
*(I →5 I e II→24 II→4) + 2 totalizando 35
*(I →4 I e II→25 II→3) + 3 totalizando 35
*(I →3 I e II→26 II→2) + 4 totalizando 35
*(I →2 I e II→27 II→ 1) + 5 totalizando 35
*(I →1 I e II→28 II→0) + 6 totalizando 35 >>>> a partir daqui não se pode tirar mais nenhum elemento de dentro dos conjuntos, pois o conjunto II ficaria negativo(-1), o que não existe.
*Dessa forma o máximo de técnicos que podem não gostar de nenhuma das atividades é 6, que é inferior a 7. Portanto:
Gabarito CERTO
-
A partir desse meu último comentário, provo que os comentários que dizem que está certo porque os que não gostam de nenhuma atividade são 0, e 0 é menor que 7, partem de um raciocínio equivocado.
-
O único jeito de entender essa questão, ou pelo menos a forma mais lógica é do jeito que o JASEN fez.
-
O jeito do Jasen não está correto, visto que o valor de x encontrado por ele é uma SUPOSIÇÃO, e não uma certeza. Podemos sim ter aqueles que não gostam de nenhuma das duas atividades.
Fiz da seguinte maneira:
x= intersecção
y= os que não gostam de nenhuma das duas atividades
Assim, x + 29-x + 28-x + y= 35
29 + 28-x + y= 35
-x + y= 35 - 29 - 28
-x + y = - 22 (multiplica por -1)
x - y = 22
x = 22 + y
Ora, se y for 7, x será igual a 29. Assim, se os que gostam somente da atividade I é 29 - x, teremos 29 - 29. Ou seja, nenhuma pessoa do grupo gosta apenas da atividade I. Até aí é possível, mas, ao aplicarmos aos que gostam somente da atividade II, teremos 28 - 29 = -1. O resultado negativo não é possível. Por isso, o valor é inferior a 7 (6 ou menos).
-
https://www.youtube.com/watch?v=R4XeRZ0f0g8
Galera achei este vídeo do professor Bruno Lima.
Ele não resolve está questão mais sim uma questão muito parecida "no momento 24 minuto do vídeo" Vocês adiantam o vídeo e vai chegar em umas resoluções muito aproveitáveis .
Espero que ajudem.
-
Eu só fiz o valor total que é 35 menos o valor maior da atividade II que é 29 = 6 então esta correta a acertativa...
-
Vamos pedir resoluções em vídeo!
Clica na explicação do profº e em seguida em Não gostei. depois justifica: quero explicações em vídeo!
-
Esse professor é um ogro não sabe explicar nada!!!
pela lógica da zero, logo zero é menor que 7, mas do jeito que o professor explicou fica impossível de se entender....
-
Josimar padilha do gran cursos on line resolve essa questão e explica muito bem
-
Pensei assim: o número máximo de pessoas que gostam de alguma atividade é 29 e dentro destes PODEM está os 28 que gostam da atividade II. Podemos pensar na seguinte hipótese: 28 técnicos gostam das atividades I e II e apenas 1 técnico gosta somente da atividade I, assim, cumpre-se o que a questão cita: 29 gostam da atividade I (28 + 1) e 28, da atividade II (interseção das atividades I e II). Ora, se dos 35 apenas 29 gostam de algo, no máximo 6 não gostam, logo, número inferior a 7 tornando correta a questão.
-
Sempre que você vir uma questão pedindo esse tipo de resolução, basta pegar o total e subtrair pelo valor do maior conjunto, sem mistério.
-
Obrigado pela as explicações aqui nos comentários se for depender do professor do QC tava era morto, tem uma preguiça da porra de gravar um vídeo
-
https://www.youtube.com/watch?v=Ia-slXgm1MA
ae galera todas do MPU TÉCNICO 2013 acabou o problema rs
-
Só consegui entender após ler o contário da MONICA SÁTOLO obrigado
-
Copiando o enunciado: A quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades é inferior a 7.
Na atividade I temos 29 pessoas; na atividade II temos 28 e no total temos 35. Se fizermos a conta achamos a intersecção que dá 22, mas isso não é necessário.
Para ter a QUANTIDADE MÁXIMA, precisamos colocar O MÍNIMO POSSÍVEL. É uma antítese, mas é bem simples. A explicação em escrito pode ficar confusa, mas tente colocar no papel que fica fácil de visualizar.
Temos Dois conjuntos: I com 29 pessoas, II com 28 pessoas e uma intersecção supostamente como x.
Coloque o menor valor (28) como se fosse a intersecção. No CONJUNTO I TOTAL continua com 29 e o CONJUNTO II TOTAL passa a ter 0.
Bom, 29 - 28 = 1 (ou seja, 29 do total do conjunto I - 28 da intersecção). Chegamos no valor MÍNIMO POSSÍVEL.
Agora é só tirar do total que temos o número que não gosta de nada, 35 - 29 = 6 ( ou seja, 35 técnicos no geral menos 29 pessoas que estão dentro do conjunto).
Espero ter ajudado.
-
Atividade 1 = A
Atividade 2 = B
Gostam da atividade 1 = n(A) = 29
Gostam da atividade 2 = n(B) = 28
Gostam das duas = n(A∩B)
Não gostam de nenhuma = n(Y)
Nesse tipo de questão, onde não se sabe o valor da interseção nem o valor de fora dos dois conjuntos, e a questão pede justamente esae valor de fora, deve-se buscar a pior das hipóteses. A pior hipótese é aquela em que o valor da interseção é o valor do menor conjunto, no caso da questão 28, não será 29 pois caso fosse, na hora de achar o valor dos que gostam da atividade 2 menos a interseção (28 - 29) restaria um número negativo, o que não pode ocorrer.
Então a expressao fica assim:
35 = (29-28) + 28 + (28-28) + n(Y)
35 = 29 + n(Y)
n(Y) = 6
Gabarito certo
-
Aí moçada quando a CESPE diz que o grupo não gosta de NENHUMA DAS ATIVIDADES eles estão se referindo a intersecção do grupo 1 e do grupo 2.
-
Gente.. até dá pra resolver com cálculos, mas é mais simples por raciocínio: Se 29 já responderam que gostam da atividade I, podemos supor que os 28 que gostam da atividade II são os mesmos 29 (menos 1), pois a questão não restringe nada nesse sentido. Assim, se ao menos 29 de 35 responderam, o número máximo de abstenções possível é 35-29=6, que é inferior a 7.
-
Melhor do que sair escrevendo teorias, textos e mais textos... é bom procurar uma resolução que nos faça compreender. Segue abaixo um vídeo (NEAF Concursos) uma explicação rapidinha e que (pelo menos para mim) resume a explicação. E podemos levar para outras questões pois é MUITO teórica.
https://www.youtube.com/watch?v=DSVpZCMIHkc
Espero ter ajudado!
-
O total técnicos são de 35, e que 29 gostam da atividade I e 28 gostam da atividade II,como eu não sei o valor da intersercção vamos chama-la de X, e atribuir Y para aqueles que não gostam de nenhuma dessas atividades,ficando assim :
29- x+x+28-x+y=35
Supondo que X vale 28 realizaremos a substituição na equação
29-28+28+28-28+Y=35
1+28+Y=35
29+Y=35
Y=35-29
Y=6
-
CERTO
Galera, temos 29 técnicos que gostam da atividade 1, certo ?
35-29=6
Logo, só tem como 6 técnicos (no máximo) não gostarem de nenhuma atividade.
6<7
-
Aprendi com um professor assim; Sempre que pedir a quantidade máxima de técnicos desse grupo que não gosta de nenhuma das duas atividades (ficar fora do diagrama) Pegar o menor valor (28) jogar na interseção (28),
e verificar quantos faltam para completar o diagrama II. Não falta nenhum, (0) pois são 28 mesmo.
Quantos faltam para completar o diagrama I, APENAS (1), POIS já há o (28), então, quantos faltam para completar 35? apenas (6). Essa é a reposta, o valor que fica fora.. Desenhando fica mais fácil...
-
EXPLICAÇÃO:
https://www.youtube.com/watch?v=DSVpZCMIHkc