-
Modus Ponens
P -> Q
P
---------------
P
-
eu em, ta amarrado kkkkkkkkk
-
Bote fé Matheus Sales ..heheheehehehehehehehe
-
Tomar banho de sal grosso Matheus e Fred! hehehehehe
-
ééé gente, é rir pra não chorar kkkkkkkkkkkkk
-
Que trem é esse? É de passar no pão?!!!
-
Essa foi para torar.... Meus deus
-
A regra de inferência, Modus Ponens, pode ser simbolizado formalmente da seguinte forma:
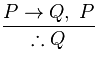
Sendo que A regra Modus ponens pode ser escrita na forma de sequentes como é mostrado a seguir:
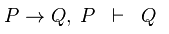
Analisando as alternativas, vemos que a correta é a letra D.
Resposta: Alternativa D.
-
Que isso
-
Nossa!!!!
-
Fácin... Sempre que vier na prova "Modus Ponens" Atente-se logo para a condicional!!
O termo antecedente é verdade se o consequente também for.
Se P implica em Q e P é verdadeira, então Q é verdadeira. Um exemplo é:
Se estiver chovendo ( P )
Encontrarei você no cinema (Q)
Se estiver chovendo, eu encontrarei você no cinema.Está chovendo.
Então, encontrarei você no cinema.
P ---> Q, P
-----------------
.:. Q
Mesma coisa da letra "D" . É só atribuir alguma frase ou hipótese.
LEMBRANDO QUE O SIMBOLO >> |- Não é uma negação, e sim como se fosse uma divisão.
-
Não entendi nem com a explicação do nosso colega, kkkkkk
Fico com a resposta que é de passar no pão! Alguém socorre!!!
-
Gente do céu! hahahaha
-
Esse início aí cheio de bobagens no enunciado é só pra intimidar o candidato. O modus ponens é simplesmente: se P é verdade, Q também será verdade. Se P for falso, Q também será falso. Já no modus tollens, ocorre o contrário: se Q for verdade, Q também será verdade. Se Q for falso, P também será falso.
-
RESOLUÇÃO:
Observe a condicional p -> q. Para esta condicional ser verdadeira, sabemos que:
- se pudermos AFIRMAR que p é V, então concluímos que q também precisa ser V (caso contrário cairíamos numa condicional falsa). Este é o Modus Ponens, ou modo de afirmar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: p
Conclusão: q
Resumindo o modus ponens em uma linha: p, p->q |- q (letra D).
- se pudermos dizer que a NEGAÇÃO de q é V (ou seja, q é F), então concluímos que p precisa ser F também (caso contrário cairíamos numa condicional falsa). Isto é, concluímos que ¬p é V. Este é o Modus Tollens, ou modo de negar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: ¬q
Conclusão: ¬p
Resumindo o modus tollens em uma linha:¬q, p -> q |- ¬p.
Resposta: D
-
Observe a condicional p -> q. Para esta condicional ser verdadeira, sabemos que:
- se pudermos AFIRMAR que p é V, então concluímos que q também precisa ser V (caso contrário cairíamos numa condicional falsa). Este é o Modus Ponens, ou modo de afirmar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: p
Conclusão: q
Resumindo o modus ponens em uma linha: p, p->q |- q (letra D).
- se pudermos dizer que a NEGAÇÃO de q é V (ou seja, q é F), então concluímos que p precisa ser F também (caso contrário cairíamos numa condicional falsa). Isto é, concluímos que ¬p é V. Este é o Modus Tollens, ou modo de negar, que nos permite escrever o argumento:
Premissa1: p -> q
Premissa2: ¬q
Conclusão: ¬p
Resumindo o modus tollens em uma linha:¬q, p -> q |- ¬p.
Resposta: D
-
Não tinha a mínima ideia dessa
-
Colocar a fórmula na horizontal quebrou minhas pernas :/ fiquei perdida kkkkk