-
http://www.tecconcursos.com.br/artigos/resolucao-da-prova-icms-rj-raciocinio-logico tem uma exelente explicação neste site, aos 12 minutos
-
Gabarito letra D. Somando as quantidades que assinam X, Y e Z, e subtraindo as interseções (XY, XZ e ZY) pois foram somadas duas vezes, achamos a quantidade de pessoas que assinam as 3 revistas (10%), depois é só montar o diagrama.
-
alguem pode explicar melhor
-
Vocês também encontram a resolução para essa questão com o professor Bruno Lima do Ponto dos Concursos.
https://www.youtube.com/watch?v=L0J4OAiGjxw
-
VOU TENTAR, MAS SABEMOS NÓS QUE É COMPLICADO TRANSFORMAR RLM EM TEXTO.. bora
Pegamos-nos os valores de X, Y,Z
X-> 50%
Y->40%
Z-> 60%
Prontooo..kkk..somos feras..kkk.. AGORA PEGUE OS VALORES QUE ESTÃO COM INTERSECÇÃO ( x,y) ; ( x, z) ; ( y, z)
X e Y-> 20%
X e Z-> 30 %
Y e Z-> 20%
hihi.. somoss bonss... agora aplique nessa lei..--> A U B U C = A+ B+ C - ( A^B) - ( A^C) - ( B^C) + ( A^B^C) .. as letras A, B e C... saõ enfeites da formulas..poderiamos colocar na formula logo Eliellll.. ? kk.. bora.... SO SUBSTITUIR ..
X U Y U Z = 50 + 40 + 60 - 20 - 30- 20 + x( esse bichinho aqui é essencial.. vamos descobri-lo)
AHHHH... O valor do X U Y U Z = 100 % né ? SO QUE A QUESTÃO FALA QUE 10% NAO ASSINA NADA, ou seja 100 - 90 = X U Y U Z = 90 % .... arroche la na formula quase pronta...
90 = 50 + 40 + 60 - 20 - 30- 20 + x 90= 80 + x.. LOGO X = 10 %
UFA NE.. prontooo.. temos a intersecção dos 3 agora...é so aplicar o diagrama de venn..PRIMEIRO AKI... NAS INTERSECÇÕES DE APENAS DUAS ASSINATURAS.
X e Y-> 20% - ( 10% ) = 10 %
X e Z-> 30 % - ( 10% ) = 20 %
Y e Z-> 20% - ( 10%) = 10 %
COMO A QUESTÃO QUER.... AS PESSOAS QUE TÊM MAIS DE UMA ASSINATURA...pegue as INTERSEÇÕES NE? ora mais.. que facil... INTERSEÇÃO É MAIS DE UM NE..cracoooo...
X e Y-> 20% - ( 10% ) = 10 %
X e Z-> 30 % - ( 10% ) = 20 %
Y e Z-> 20% - ( 10%) = 10 %
COMO A QUESTÃO QUER.... 10 + 20 + 10 + ( os 10 da interseção.. lembrado) = 50 %
GABARITO DESSA PORRA..KK..D
-
50% + 40% + 60% = 150%
Considerando que existem três possibilidades de assinaturas (x, y, z) (xy, xz, yz) (xyz), devemos efetuar o seguinte calculo:
150% / 3 = 50% para cada possibilidade de assinatura.
150% = Percentual de empregados que assinam revistas;
3 = Nº de possibilidades de assinaturas.
-
PASSO A PASSO
Vamos aos dados FORNECIDOS
pela questão:
X
= 50%
Y
= 40%
Z
= 60%
X
e Y = 20%
X
e Z = 30%
Y
e Z = 20%
Não
assinaram (X e Y e Z) = 10%
Participaram
da pesquisa = 100% (não
foi fornecido, porém estamos tratando de porcentagem. 10% de alguma coisa, só
pode ser 10% de 100%, ok!?)
Os
empregados que assinaram (X e Y e Z) = ? não sabemos o valor! (podemos chamar de x ou a letra que você quiser!)
***************************************************************************************************
*Achei que o uso dessa
fórmula ajuda bastante quando falta APENAS o x. Não se assustem com o tamanho!! É grande, porém seu entendimento
é MUITO fácil!
***************************************************************************************************
Fórmula: n (X U Y U Z) = n (X) + n (Y) + n
(Z) - n (X ∩ Y) - n (X ∩ Z) - n (Y ∩ Z) + n (X ∩ Y ∩ Z)
***************************************************************************************************
Traduzindo:
n
(X U Y U Z) = número da união dos elementos dos três conjuntos
Não assinaram (X e Y e Z)
= 10%
Participaram da pesquisa
= 100% (não foi fornecido, porém estamos
tratando de porcentagem. 10% de alguma coisa, só pode ser 10% de 100%, ok!?)
Logo, 100% – 10% = 90%
n
(X U Y U Z) = 90%
n
(X) = 50%
n
(Y) = 40%
n
(Z) = 60%
n
(X ∩ Y) = 20%
n
(X ∩ Z) = 30%
n
(Y ∩ Z) = 20%
n
(X ∩ Y ∩ Z)= Os empregados
que assinaram (X e Y e Z) = ? não
sabemos o valor! (podemos chamar de x
ou a letra que você quiser!)
***************************************************************************************************
n
(X U Y U Z) = n (X) + n (Y) + n (Z) - n (X ∩ Y) - n (X ∩ Z) - n (Y ∩ Z) + n (X ∩
Y ∩ Z)
90%
= 50% + 40% + 60% - 20% - 30% - 20% + x
90%
= 80% + X
90%
- 80% = X
10%
= X
(achamos
o valor de x), ou seja, os empregados que assinaram (X , Y e Z) = 10%
***************************************************************************************************
Depois que achei o x
(10%), ou seja, os empregados assinantes das revistas X, Y e Z
Fiz assim:
Somei os empregados que assinam mais de uma revista.
Empregados assinantes da
revista X e Y = 20% MENOS 10% (do x que
achei) é igual a 10%
Empregados assinantes da
revista X e Z = 30% MENOS 10% (do x que
achei) é igual a 20%
Empregados assinantes da
revista Y e Z = 20% MENOS 10% (do x que
achei) é igual a 10%
Logo,
10% (do x que achei)+ 10% + 20% + 10% = 50%
50%
é a resposta!
-
50%+40%+60% = 150% - 100% = 50%
X ∩ Y = 20 X ∩ Z = 30 X ∩ Y = 20****
20-x + 30-x + 20-x + x = 50
70 - 2x = 50x****
x=10=X∩Y∩Z
100%-10%= 90%
100%= Total de pessoas
10%= pessoas que não assinam nenhuma revista
90%= Total de assinantes
Somente X = 50-10-10-20 = 10
Somente Y = 40-10-10-10 = 10
Somente Z = 60-10-10-20 = 20
-
uma forma mais rapida...
vc soma quem esta sozinho x+y+z (50+40+60=150) com quem esta de fora (10) = 160
e diminue de quem faz pares x&y + y&z + x&z (20+30+20) = 70
160-70 = 90... esses 90% vc diminue de 100% e acha o valor que é comum aos 3... no caso x&y&z = 10%
a parte dificil é essa...dai é so aplicar no diagrama....
-
não assinantes=10%
assinantes= 100%-10%=90%
90=50+40+60-20-30-20+x
90=80+x
x=10%
x e y=20-10=10%
x e z=30-10=20%
y e z=20-10=10%
x=10%
10+20+10+10=50% assinam mais que uma revista
-
De acordo com o enunciado, temos:
n(X) = 50%
n(Y) = 40%
n(Z) = 60%
n(X∩Y) = 20%
n(X∩Z) = 30%
n(Y∩Z) = 20%
10% não assinam e W = n(X∩Y∩Z)
Logo:
n(X∪Y∪Z) = n(X) + n(Y) + n(Z) - n(X∩Y) - n(X∩Z) - n(Y∩Z) + W
Substituindo os valores, onde n(X∪Y∪Z) = 100% - 10% (que não assinam nada) = 90%
90 = 50 + 40 + 60 - 20 - 30 - 20 + w
w = 10%
Fazendo o Diagrama de Venn:
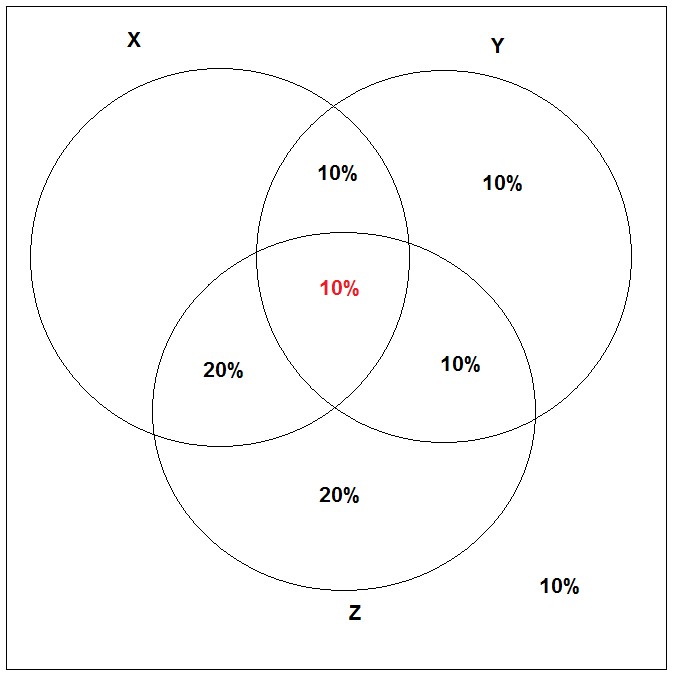
Assim, a porcentagem dos empregados que assinam mais que uma revista é igual a:
10% + 20% + 10% + 10% = 50%
Resposta: Alternativa D.
-
TOTAL DE ASSINANTES = 90%
NÃO SÃO ASSINANTES = 10%
X = 50%
Y = 40%
Z = 60%
X e Y = 20%
X e Z = 30%
Y e Z = 20%
n (X U Y U Z) = n (X) + n (Y) + n (Z) - n (X ∩ Y) - n (X ∩ Z) - n (Y ∩ Z) + n (X ∩ Y ∩ Z)
90% = 50% + 40% + 60% - 20% - 30% - 20% + x
90% = 80% + x
x = 10%(intersecção)
obtém-se que a porcentagem dos empregados que assinam MAIS QUE UMA revista é igual a
X e Y = 20% - 10%(intersecção) = 10%
X e Z = 30% - 10%(intersecção) = 20%
Y e Z = 20% - 10%(intersecção) = 10%
X e Y e Z = 10%(intersecção)
INTERSECÇÃO + (X e Y) + (X e Z) + (Y e Z)
10% + 10 + 20% + 10% = 50%
GABARITO D
-
Aproveitando para deixar minha contribuição...
Gabarito: Letra D;
Inicialmente, vamos organizar os dados fornecidos pela questão:
X =
50%; Y =
40%; Z =
60% ----- 50 + 40 + 60 = 150
X e Y =
20%; X e Z = 30%; Y e Z
= 20% ----- 20 + 30 + 20 = 70
Não são assinantes:
10%
X
e Y e Z = ? (A questão não nos forneceu a intersecção entre os três conjuntos)
Aplicando
o macete “TODOS MENOS 2”, sabendo
que o total é 100% e admitindo que a intersecção entre os 3 conjuntos é x, encontramos
o valor dessa intersecção. Veja:
150
+ 10 – 70 + x = 100 --- 90 + x = 100
---- x = 10%
Como
a questão nos pede a porcentagem dos empregados que assinam mais que uma revista, sabe-se
que a resposta será a soma
daqueles que assinam SOMENTE
as duas revistas com aqueles que assinam as três revistas. Logo, precisamos
encontrar o valor daqueles que assinam somente duas revistas. Portanto:
Se
X e Y = 20%, temos que 20% - 10 % = 10% assinam somente X e Y;
Se
X e Z = 30%, temos que 30% - 10 % = 20% assinam somente X e Z;
Se
Y e Z = 20%, temos que 20% - 10 % = 10% assinam somente Y e Z;
Solução: 10% + 20% + 10% + 10% = 50 % assinam mais de duas
revistas.
Conheçam e inscrevam-se no meu canal no youtube, pois sou professor de Matemática e gravei alguns vídeos com dicas e bizus de Matemática e Raciocínio Lógico.
Link do canal: https://www.youtube.com/channel/UC_FQm8aivYBf2q6ga1rxklw?sub_confirmation=1
Fanpage: https://www.facebook.com/profjuliocesarsalustino
-
a izabel pereira deixou um link no you tube que explica tudo de uma maneira bem facil , nao tava entendendo bem mas consegui compreender deem uma olhada e vcs irao enteder valeu isabel !!!
-
entendi com a explicação da Elaine!!!
-
Seguinte:
X= 50%
Y= 40%
Z= 60%
Temos um total de 150%.
Ou seja, se sabemos que o total de empregados precisa ser necessariamente 100%, temos que 50% das pessoas estão sendo contadas duas vezes! Concluo, então, que são exatamente esses 50% que assinam mais de 1 revista.
Então a resposta é 50%. Fácil e rápido. Só usando a lógica e interpretação.
-
Corrijam- me se estiver errado como ele deu 50%, 40% 60% vc soma esses três (40 + 60 + 50 = 150) opa passou de 100%, ou seja, o que passou são as interseções que foi o que a questão cobrou 50%
-
Gabarito D
A explicação da questão está no link abaixo.
https://youtu.be/MQzAfI51lLs?t=29105
fonte: 3ª Maratona ALECE: Técnico Legislativo Pós-Edital - prof. Carlos Henrique - Estratégia Concursos
-
Gabarito:D
Principais Dicas:
- Principais questões são de 2 ou 3 conjuntos.
- Primeiro acha sempre a intersecção e sai complementando. Ex: A ∩ B = 10; A= 20; B=30. Logo, A tem apenas 10 e B tem apenas 20.
- Caso não tenha a intersecção? Soma tudo e subtrai do total. Ex: A= 20; B=30; Total= 40. Logo, a intersecção é 50-40=10.
- E cuidado nas questões que ele fala APENAS, SOMENTE etc.
FICA A DICA: Pessoal, querem gabaritar todas as questões de RLM? Acessem tinyurl.com/DuarteRLM .Lá vocês encontraram materiais produzidos por mim para auxiliar nos seus estudos. Inclusive, acessem meu perfil e me sigam lá pois tem diversos cadernos de questões para outras matérias. Vamos em busca juntos da nossa aprovação juntos !!
-
Precisamos entender que há funcionários que assinam as 3 simultaneamente.
A fórmula --> t = x+y+z-i2+i3 pode nos ajudar
i2 = interseção de 2
i3 = interseção de 3
t= total, que é 100
Porém, apenas 90 entram na contagem dos assinantes:
90=(50+40+60)-(20+30+20)+i3
90 = 150 - 70 + i3
90=80+i3
i3 = 90-80
i3 = 10
10 pessoas assinam as 3 simultaneamente.
XeY = 20, porém já temos 10 --> completamos com mais 10
Yez = 20, porém já temos 10 --> completamos com mais 10
XeZ = 30, porém já temos 10 --> completamos com mais 20.
O enunciado pede quem assina mais de uma, ou seja, i2+i3
i3=10
i2 = 40
resultado = 50%
GABARITO D